
Читайте также:
|
| Определение Пр.1.3.1. |
Кривая, уравнение которой в некоторой ортонормированной системе координат имеет вид 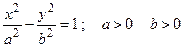 , называется гиперболой. , называется гиперболой.
|
| Определение Пр.1.3.2. |
Число  называется эксцентриситетом гиперболы.
Точки называется эксцентриситетом гиперболы.
Точки  называются фокусами гиперболы.
Прямые называются фокусами гиперболы.
Прямые 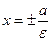 называются директрисами гиперболы.
Число называются директрисами гиперболы.
Число 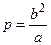 называется фокальным параметром гиперболы. называется фокальным параметром гиперболы.
|
Cвойства гиперболы:
1°. Гипербола - неограниченная кривая, существующая для  , что следует из записи канонического уравнения в форме
, что следует из записи канонического уравнения в форме 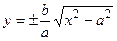 ;
;
2°. Гипербола L обладает осевой симметрией относительно осей Ox и Oy, а также центральной симметрией относительно начала координат. Это вытекает из отношений
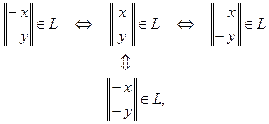 ,
,
очевидных для канонического уравнения гиперболы.
Через α и β обозначим углы между касательной и фокальными радиусами (рис. Пр.1.3.1.)
| Определение Пр.1.3.2. |
Прямая  называется асимптотой для линии называется асимптотой для линии 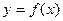 при при 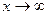 , если , если
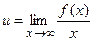 и
и
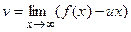 . .
|
3°. Гипербола обладает асимптотами вида 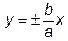 .
.
 Свойства гиперболы иллюстрируются
рис. Пр.1.3.1. Свойства гиперболы иллюстрируются
рис. Пр.1.3.1.
| 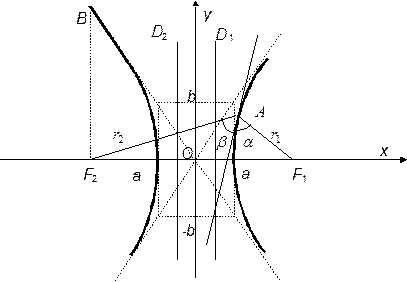 Рисунок Пр.1.3.1.
Рисунок Пр.1.3.1.
|
Действительно,  и, кроме того,
и, кроме того,

| Теорема Пр.1.3.1. | Пусть A = 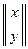 есть точка, принадлежащая гиперболе L, заданной каноническим уравнением, тогда имеют место следующие соотношения:
1°. Для правой ветви есть точка, принадлежащая гиперболе L, заданной каноническим уравнением, тогда имеют место следующие соотношения:
1°. Для правой ветви
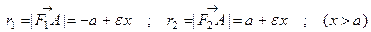 .
Для левой ветви .
Для левой ветви

|
2°.  3°. 3°.  4°.
4°.  5°. 5°.  6°.
6°.  . .
|
Доказательство:
1°. Доказательство аналогично доказательству теоремы Пр.1.2.1., поэтому ограничимся здесь лишь нахождением величин
 ,
используя каноническое уравнение и определение эксцентриситета.
Для ,
используя каноническое уравнение и определение эксцентриситета.
Для  получаем получаем

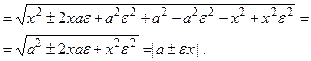 Но поскольку для гиперболы
Но поскольку для гиперболы  и и  , то для правой ветви , то для правой ветви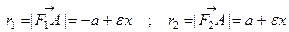 ,а для левой - соответственно ,а для левой - соответственно  .Откуда и следует 2° и 3°.
Справедливость 4° докажите самостоятельно.
5°. Наконец, .Откуда и следует 2° и 3°.
Справедливость 4° докажите самостоятельно.
5°. Наконец, 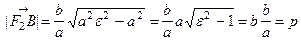 .
6°. Докажите это утверждение самостоятельно, по аналогии с доказательством свойства 6° теоремы Пр.1.2.1., используя также теорему Пр.1.3.1.
Теорема доказана. .
6°. Докажите это утверждение самостоятельно, по аналогии с доказательством свойства 6° теоремы Пр.1.2.1., используя также теорему Пр.1.3.1.
Теорема доказана.
|
Замечание о свойствах гиперболы:
Каноническое уравнение, изучаемой в курсе элементарной математики гиперболы  , получается путем следующей замены координат
, получается путем следующей замены координат
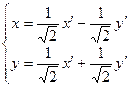 .
.
Из теорем Пр.1.3.1. и Пр.1.2.2. следует возможность альтернативных формулировок свойств гиперболы.
Фокальное свойство гиперболы: гипербола есть геометрическое место точек, абсолютная величина разности расстояний от которых до двух фокусов, постоянна и равна 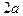 .
.
Директориальное свойство гиперболы: гипербола есть геометрическое место точек, отношение расстояния от которых до данной точки (фокуса) к расстоянию до данной прямой (директрисы) постоянно и больше единицы.
Оптическое свойство гиперболы: касательная в любой точке гиперболы образует с фокальными радиусами точки касания равные углы. (Изображение точечного источника света, расположенного в одном из фокусов, есть мнимое и находится в другом фокусе гиперболы.)
Проведение касательных к гиперболе
| Теорема Пр.1.3.2. | Пусть A =  есть точка, принадлежащая гиперболе, заданной каноническим уравнением, тогда уравнение касательной к этой гиперболе, проходящей через точку А, имеет вид: есть точка, принадлежащая гиперболе, заданной каноническим уравнением, тогда уравнение касательной к этой гиперболе, проходящей через точку А, имеет вид:
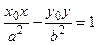 . .
|
Доказательство:
Уравнение касательной в точке A имеет вид 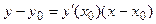 .
Для гиперболы из канонического уравнения получаем .
Для гиперболы из канонического уравнения получаем 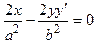 , то есть , то есть  . Но тогда . Но тогда  , принимая во внимание, что , принимая во внимание, что  , окончательно получим , окончательно получим 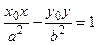 .
Наконец, непосредственно проверяем утверждение теоремы для точек .
Наконец, непосредственно проверяем утверждение теоремы для точек 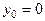 , где уравнения касательных имеют вид , где уравнения касательных имеют вид 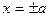 .
Теорема доказана. .
Теорема доказана.
|
Уравнение гиперболы в полярной системе координат
 Поместим полюс полярной системы координат в правый фокус гиперболы, а полярную ось направим по положительной полуоси Ox. (Рис. Пр.1.3.2.)
Имеем для произвольной точки A, лежащей на правой ветви гиперболы, Поместим полюс полярной системы координат в правый фокус гиперболы, а полярную ось направим по положительной полуоси Ox. (Рис. Пр.1.3.2.)
Имеем для произвольной точки A, лежащей на правой ветви гиперболы,
 Откуда
Откуда  и окончательно и окончательно 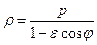 . .
| 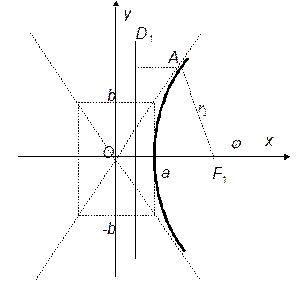 Рисунок Пр.1.3.2.
Рисунок Пр.1.3.2.
|
Дата добавления: 2015-09-10; просмотров: 147 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Пр.1.2. Эллипс и его свойства | | | Пр.1.4. Парабола и ее свойства |