
Читайте также:
|
Каноническое уравнение параболы в прямоугольной системе координат:
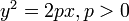 (или
(или  , если поменять местами оси).
, если поменять местами оси).
Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии  от обоих.
от обоих.
| [показать]Вывод |
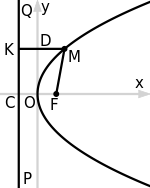
 Уравнение директрисы
Уравнение директрисы  : : 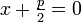 , фокус — , фокус —  , таким образом начало координат , таким образом начало координат  — середина отрезка — середина отрезка  . По определению параболы для любой точки . По определению параболы для любой точки  , лежащей на ней выполняется равенство , лежащей на ней выполняется равенство  . .  и и  , тогда равенство приобретает вид: , тогда равенство приобретает вид:
 .
После возведения в квадрат и некоторых преобразований получается равносильное уравнение .
После возведения в квадрат и некоторых преобразований получается равносильное уравнение  . .
|
Квадратное уравнение  при
при 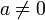 также представляет собой параболу и графически изображается той же параболой, что и
также представляет собой параболу и графически изображается той же параболой, что и  , но в отличие от последней имеет вершину не в начале координат, а в некоторой точке
, но в отличие от последней имеет вершину не в начале координат, а в некоторой точке  , координаты которой вычисляются по формулам:
, координаты которой вычисляются по формулам:
 где
где  — дискриминант
— дискриминант
Ось её симметрии проходит через вершину параллельно оси ординат, при a>0 (a<0) фокус лежит на этой оси над (под) вершиной на расстоянии a/4, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение  может быть представлено в виде
может быть представлено в виде  , а в случае переноса начала координат в точку
, а в случае переноса начала координат в точку  каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим. При этом
каноническим уравнением. Таким образом для каждого квадратного уравнения можно найти систему координат такую, что в этой системе оно представляется каноническим. При этом  .
.
Дата добавления: 2015-09-10; просмотров: 72 | Поможем написать вашу работу | Нарушение авторских прав |