Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Електронний газ при . Сфера Фермі

Вільні електрони в металі можна розглядати як частинки в потенціальному ящику, які підкоряються стаціонарному рівнянню Шредінгера з відповідними граничними умовами:

Електрони в потенціальному ящику вважаються вільними, тому всередині металу . Для простоти розглянемо металевий зразок, як паралелепіпед.

Щоб описати стан електрона в металі, необхідно задати граничні умови. Макроскопічні властивості металу не залежать від конкретного вигляду граничних умов, тому їх вибирають із міркувань математичної зручності. Простий фізичний зміст мають такі граничні умови:

(ящик з нескінченно високими стінками)

Однак найчастіше користуються періодичними граничними умовами Борна-Кармана.

Спочатку знайдемо загальні розв'язки.

довільним розв'язком є , де напрям довільний, а

Подіємо на функцію оператором проекції імпульсу тобто Власне значення. Отже, хвильова функція описує квантовий стан електрона з імпульсом ( - хвильовий вектор), цьому імпульсу відповідає довжина хвилі Невизначеність координати , тоді маємо невизначеність імпульсу , цьому відповідає невизначеність хвильового вектора . Врахуємо граничні умови Борна-Кармана:

аналогічно

Граничні умови накладають обмеження на хвильовий вектор. Вони роблять спектр дискретним. Множину і дозволених станів електрона в металі зручно зображати векторами, або точками оберненого простору, який, називають к-простором. Всі дозволені стани системи електрона утворюють у к- просторі регулярну сітку вузлів із періодами

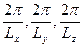вздовж відповідних осей. Таким чином, на кожен вузол такої сітки припадає одна комірка у вигляді паралелепіпеда

зі сторонами 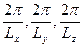тобто на кожен дозволений стан електрона приходиться об’єм

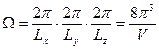в к – просторі. В силу співвідношення Гейзенберга стан електрона

розмазаний по цій комірці. Згідно принципу Паулі в кожній комірці не може перебувати більше двох електронів. Розглянемо тепер електронний газ вільних і незалежних електронів «при абсолютному нулі» (тобто при достатньо низькій температурі). При кожен електрон намагається зайняти квантовий стан з найменшою енергією, тобто ближче до центру ^-простору, а відстанню до центра є хвильове число к, яке визначає енергію електрона В силу принципу Паулі електрони займають певний об'єм навколо центру k - простору вигляді кулі; границя цієї кулі називається сферою Фермі. Знайдемо радіус сфери загальна кількість електронів у металі, 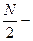кількість заповнених комірок,

отже.

Енергія Фермі - це максимальна енергія електрона при абсолютному

нулі температури,

Швидкість Фермі м/с

Отже, навіть при рух не завмирає, електрони «гасають»

по металу з швидкостями під мільйон метрів за секунду. Причина цього - принцип Паулі.

Отже, можна чекати дифракції електронів на решітці.