Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Решітка Браве

Кристал можна уявити як впорядковане розміщення атомів. Основна ознака кристалу - це трансляційна симетрія, тобто періодичність у трьох напрямках з певними періодами .

Кристал - це решітка Браве + базис. Базис - це комбінація атомів біля певного вузла решітки, яка повторюється від вузла до вузла.

Решітка Браве - це множина точок (вузлів), радіус-вектори яких є лінійною комбінацією трьох базисних векторів з цілочисельними коефіцієнтами

Базисні вектори називаються породжуючими. Об'єм, що приходиться на кожен вузол решітки Браве і періодично повторюється, називається примітивною коміркою решітки Браве. Таким чином, примітивна комірка містить один вузол. Вибір примітивної комірки неоднозначний.

Найбільш повно відображає симетрію решітки так звана комірка Вігнера-Зейтца. Комірка Вігнера-Зейтца - це геометричне місце точок, більш близьких до даного вузла, ніж до всіх інших.

Більшість кристалічних решіток, крім трансляційної симетрії (інваріантність решітки відносно переносу на ціле число породжуючих векторів), мають поворотну симетрію. Поворотна симетрія кристалу описується за допомогою вісі симетрії, при повороті навколо якої на кут 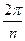кристал накладається сам на себе.

Теорема. Кристали можуть мати поворотні осі симетрії лише таких порядків п = 1,2,3,4,6.

Це обмеження на поворотні осі симетрії накладається трансляційною симетрією.

Доведення. Розглянемо два сусідніх вузли решітки Браве, відстань між якими дорівнює одному із періодів решітки. Проведемо вісь поворотної симетрії через вузол 1 і повернемо кристал перпендикулярно площині малюнку на кут проти годинникової стрілки. Тоді вузол 2 а накладеться на вузол 1 Внаслідок трансляційної симетрії, таку ж вісь можна провести через вузол 2, і повернути кристал за годинниковою стрілкою. За побудовою видно, що 1’2//12, тому ми маємо рівнобедренну трапецію. В силу трансляційної симетрії, довжина відрізка 1'2', кратна періоду а 1'2'= та, де , з іншого боку, але то очевидно, що т може набувати лише значень

На початку 70-х років було знайдено ряд сплавів, які мали поворотну вісь симетрії 5-го порядку. Потім були відкриті тверді тіла з забороненими осями 10-го та 12-го порядків. Такі сплави стали називати квазікристалами. Квазікристали не мають трансляційної симетрії, але мають дальній порядок. У математичному плані квазікристали описуються за допомогою квазіперіодичних функцій, які характеризуються кількома

періодами, відношення яких ірраціональне. Решітки Браве можна класифікувати використовуючи поняття симетрії. Існує 14 типів решіток Браве, які згруповані у 7 класів (сингоній). Кожну решітку характеризують елементарною коміркою. Це певна сукупність вузлів, повторення яких дає всю решітку.

1) Кубічна сингонія

2) Тетрагональна сингонія ;

3) Ромбічна сингонія

4) Моноклинна сингонія

5) Триклинна сингонія ;

6) Тригональна сингонія

7) Гексагональна сингонія

Найбільш розповсюджений клас - це кубічні решітки Браве, яких існує три типи: - прості кубічні, - об'ємно-центрована кубічна (ОЦК), - гранецентрована кубічна (ГЦК). До найбільш розповсюджених решіток також відноситься гексагональна щільно упакована решітка (ГЦУ).

Елементарну комірку решітки можна вибрати по різному. У простій решітці (й елементарна комірка не має вузла всередині) об'єми таких комірок однакові і на кожну з них припадає по одній частинці (вузол припадає на 8 комірок, але вершин-вузлів у комірці 8, тому . Щоб елементарна комірка найбільшою мірою 8 відображала симетрію всього кристалу, часто вибирають комірку так, щоб додаткові вузли містилися в центрах граней або в центрі її об'єму.

ОЦК решітка, тобто на кожну комірку припадає дві частинки (атоми). Кількість найближчих сусідів дорівнює 8. Відстань між найближчими сусідами Кристалічну структуру розглядають як правило в моделі твердих сфер. Кожен атом вважається твердою сферою радіусом R. Найближчі атоми дотикаються, так що Тоді ступінь заповнення комірки кулями Отже, пустоти між атомами займають 32%. ОЦК - решітку мають метали - хром, титан, молібден, вольфрам, цирконій, залізо в певному інтервалі температур. Пустота по кристалу розподілена нерівномірно, основна її доля приходиться на октаедричні та тетраедричні пустоти. Визначимо максимальний розмір домішкового атома, який може поміститися в октаедричній пустоті

Поміститися лише ті атоми, радіус яких складає не більше 17%

радіуса основного атома. Це домішки - водень, кисень, вуглець.

ГЦК решітка. тобто на кожну комірку припадає чотири атоми. Кількість найближчих сусідів дорівнює 12. Відстань між найближчими сусідами Ступінь заповнення комірки кулями ГЦК решітка - це найбільш компактна решітка.

Зрозуміло, що вільний об'єм розподілений у просторі нерівномірно. Найбільш "просторим" місцем в ГЦК - комірці є й центр, найближче до якого симетрично розміщені шість атомів на гранях елементарної комірки, які утворюють правильний октаедр.

Тому така пустота називається октаедричним міжвузіллям, і може вмістити атом радіусом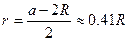

Таким чином, домішковий атом малих розмірів легко вміщується в октаедричному міжвузіллі.

Крім октаєдричної пустоти в центрі елементарної комірки, існує вільний об'єм між будь-якими чотирма сусідніми кулями, що є вершинами правильного тетраедра. Відповідно такий міжвузілля називається тетраедричним і має об'єм

ПЩУ решітка. Гексагональна щільно упакована решітка не є решіткою Браве, це решітка з базисом. Елементарна комірка - це шестикутна правильна призма, в центральній площині якої міститься ще три атоми, які одночасно дотикаються до атомів

верхньої і нижньої основ. тобто на кожну комірку припадає шість атомів. Кількість найближчих сусідів дорівнює 12. Пропонуємо читачу пересвідчитись, що ступінь заповнення для цієї решітки співпадає з ГЦК решіткою, а відношення висоти призми до сторони правильного шестикутника

2. Існує взаємна відповідність між векторами оберненої решітки і сімействами атомних площин прямої решітки. Атомна площина - це площина, що містить, як мінімум, три вузли решітки Браве. Сімейство атомних площин - це множина паралельних атомних площин, які в сукупності містять всі вузли решітки Браве.

Теорема.

Кожному сімейству атомних площин з між площинною відстанню d відповідає вектор оберненої решітки, перпендикуляр­ний до цих площин і рівний по величині , —одиничний вектор нормалі до площин сімейства. Доведення Покажемо, що вектор належить оберненій решітці. Для цього розглянемо дві довільні площини сімейства. Нехай вектор прямої решітки з'єднує довільні два вузли. Очевидно, що скалярний добуток , АВ— відстань між площинами, отже відстань кратна d, оскільки ці дві площини належать сімейству: АВ = тd. Тому шуканий скалярний добуток . Це справедливо для будь-якого вектора прямої решітки . Це і означає, що належить оберненій решітці. Існує, також і зворотній зв'язок: кожному вектору оберненої решітки відповідає сімейство атомних площин нормальних (перпендикулярних) до цього вектора. Міжплощинна відстань визначається з наступних міркувань: нехай довільний вектор оберненої решітки, тобто . Якщо , , мають спільний множник, то винесемо його за дужки: 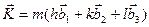де h,k,l— не мають спільного множника. Позначимо вираз в дужках - це найменший із векторів оберненої решітки, паралельний . Тоді міжплощинна відстань . Коефіцієнти h,k,l, які не мають спільних множників, називаються індексами Міллера.