Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Магнитное взаимодействие как релятивистский эффект

Покажем, что магнитное взаимодействие двух движущихся зарядов возникает лишь в том случае, если это движение наблюдать из системы отсчета, не связанной с зарядами. Если же наблюдатель движется вместе с зарядами прямолинейно и равномерно со той же скоростью , то все явления протекают так, как если бы система покоилась, то есть сила взаимодействия с его точки зрения будет только кулоновской. Этого требует принцип относительности, сформулированный еще Галилеем для механических явлений и обобщенный Эйнштейном на все явления, включая и электромагнитные.

Чтобы не только доказать появление магнитной силы при переходе из одной системы отсчета в другую, но и получить соответствующее опыту выражение для нее, нам потребуется только два хорошо известных вывода теории относительности:

1. Время минимально в той системе, где происходит событие.

2. Масса минимальна в той системе, где тело покоится.

Приведём соответствующие этим выводам формулы:

(5.18) и (5.46).

(3.2)

Номера, стоящие возле каждого выражения, принадлежат уравнениям, введённым в 1 части курса лекций.

А теперь рассмотрим мысленный опыт, изображенный на рис. 3.1. Речь пойдет о тех же двух зарядах одного знака, которые движутся с одинаковой скоростью параллельно друг другу и их движение можно принять за два параллельно текущих тока. Мы помним, что эти токи должны притягиваться, взаимодействуя своими магнитными полями. На рис. 3.1 показаны силовые линии заряда q ₁, который создает поле. Сила, действующая на заряд q ₂, попавший в это поле, будет кулоновой для того наблюдателя, который находится в системе К^¢ и движется вместе с зарядами со скоростью u в направлении оси Х. Эта сила взаимодействия может быть записана так:

и ,

(3.3)

где ' — напряжённость поля точечного заряда q₁, а 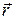— вектор, проведённый от заряда, создающего поле, в ту его точку, где находится заряд q₂, т.е. перпендикулярно скорости движения зарядов (см. рис 3.1).

Чтобы найти силу , которая действует на заряд q ₂ с точки зрения наблюдателя, находящегося в лабораторной системе отсчета К, запишем второй закон Ньютона для этой системы, считая что масса заряда q₂ будет m в системе К и m₀ в системе К^¢, где он покоится:

,

(3.4)

где u — скорость в направлении оси oy, которую может получить заряд q ₂ под действием силы . Приращение координаты y при движении заряда вдоль этой оси будет одинаковым в обеих системах, т.е. dy = dy'. Тогда связь скоростей поперечного движения заряда может быть найдена просто заменой времени dt на dt' по первому из соотношений (3.2):

.

(3.5)

Сила теперь может быть связана с кулоновой силой ' заменой в (3.4) массы заряда m на m₀ — массу заряда в той системе, где он покоится; времени dt на dt' и скорости u на u' по только что полученному соотношению, то есть

,

(3.6)

Преобразуем последнее равенство, умножив и поделив правую часть на :

.

(3.7)

Для скоростей, далеких от скорости света u << c, знаменатели» 1, и на заряд q ₂ в системе К будут действовать две противоположно направленные силы:

'.

(3.8)

Напомним, что через мы обозначили обычную силу Кулона, действующую на заряд q ₂ в системе отсчета, связанной с движущимися зарядами. С точки зрения экспериментатора, наблюдающего это движение из системы К, к взаимному отталкиванию добавится существенно меньшая по величине сила притяжения, равная силе Кулона, умноженной на отношение квадратов скоростей, т.е. магнитная сила (3.1).

Величина этой силы зависит от скорости движения, и она меньше кулоновой в u²/c² раз, а её направление противоположно силе , что соответствует результатам опыта по взаимодействию параллельных токов.