Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Вычисление напряженности магнитного поля прямого тока

Закон Био — Савара дает возможность вычислить напряженность магнитного поля, либо магнитную индукцию, созданную током, текущим по проводнику любой формы. Для этого нужно лишь просуммировать действие всех отдельных элементов тока , на которые можно разбить любой проводник. Поскольку и напряженность и магнитная индукция — величины векторные, перед тем как суммировать , следует убедиться, что эти вектора, созданные каждым элементом , направлены одинаково. Только после этого можно воспользоваться скалярным выражением закона Био — Савара и проинтегрировать его в тех пределах, для которых векторы направлены одинаково.

Рассмотрим случай бесконечно длинного прямого провода, изображенного на рис. 3.5. Весь провод вначале разбивают на элементы , два из которых выделены на рисунке. Направление элементов совпадает с направлением тока. Найти напряженность, созданную одним из элементов в точке А, где она нас интересует, можно, пользуясь законом Био — Савара. Для этого из начала вектора следует провести радиус-вектор в точку А, и указать угол a, синус которого входит в закон. Направление поля, созданного этим элементом в точке А, находится правилом буравчика. Затем следует передвигать элемент вдоль провода, проверяя каждый раз направление соответствующего . Угол a между началами векторов и 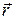при этом будет меняться: для элемента, взятого в начале провода, он стремится к нулю. Потом, постепенно возрастая, делается тупым и в пределе стремится к p. Случай, когда угол тупой, тоже изображен на рис. 3.5.

Легко видеть, что в точке А, где требуется найти напряженность, векторы , созданные всеми элементами , направлены одинаково, поэтому

H= = .

(3.19)

Пределы интегрирования пока расставить затруднительно, поскольку под знаком интеграла три переменных. Сведение их к одной можно произвести разными способами. Мы рассмотрим один из них.

Прежде всего стоящее под знаком интеграла произведение двух переменных dl и sin α дает dS — элемент окружности радиуса» r с центром в точке А, где ищется напряженность. Проведя через эту точку прямую, параллельную , мы убедимся, что этот элемент опирается на угол, который можно обозначить через d a. Значит:

dl sin α = dS = rdα и H = .

(3.20)

Опустив теперь перпендикуляр на проводник с током и обозначив его длину r sina буквой а, получим интеграл с одной переменной — углом a:

H = , и окончательно H = .

(3.21)

Пределы интегрирования взяты для случая, когда проводник бесконечный. Если же он ограничен с обеих сторон, результат интегрирования будет

H = .

(3.22)

Выражение для напряженности прямого бесконечного провода (3.21) может послужить для установления единицы измерения напряженности. В СИ она носит название, совпадающее с ее размерностью: ампер на метр (А/м). О единицах измерения магнитной индукции мы будем говорить позднее.

Разобранный выше пример расчета магнитного поля с помощью закона Био — Савара типичен, на его основе решаются многие задачи, в том числе и часто встречающиеся на практике. Существует еще одна возможность нахождения напряженности магнитного поля — теорема о полном токе. Она имеет ограниченное применение, закон же Био — Савара может быть использован в любом случае, правда, часто с серьёзными математическими затруднениями.