Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Формулировка теоремы Гауса-Маркова.

теорема Гаусса — Маркова: если в уравнении регрессии случайная компонента — белый шум, а факторы — неслучайные линейно-независимые

векторы, то несмещенные и эффективные, т.е. с минимальными дисперсия­ми, линейные оценки коэффициентов могут быть получены методом наименьших квадратов.

3а. Что такое инвариантные и неинвариантные функции? какие классы инвариантных функций существуют?

Известны три класса таких функций: степенные полиномы, синус и косинус, показа­тельные функции. Каждая функция из этих классов при изменении начала отсчета, или, иначе говоря, при сдвиге во времени, остается с точностью до линейных коэффициентов функцией того же вида, а именно: полиномы оста­ются полиномами тех же порядков, хотя и с другими коэффициентами, функции синус и косинус будут иметь те же частоты (периоды колебаний), показательные функции не изменяют своих оснований.

4. Какие показатели точности и надежности?

Точность: какую меру согласия (приближения) следует принять на данном этапе анализа, когда мы имеем дело с последовательностью не­случайных и точных величин X (1),.... X (N)? Таких мер существует много. Наиболее известные из них — критерий точного совпадения в узлах^инфор­мации, критерий Чебышева (основная его идея состоит в том, чтобы умень­шить максимальные отклонения до минимума), критерий минимизации среднего квадрата невязок.

У полинома Р(t) порядка I число неизвестных коэффициентов равно I + 1, и если оно меньше числа наблюдений N, то приближающий полином будет в общем случае (т.е. для реальной, а не специально подобранной ин­формации) отклоняться от временного ряда X (t). Минимизируя средний квадрат отклонений (невязок) для каждого I из диапазона [1, N — 2], мы получим совокупность оцененных полиномов Р(t), 1 = 1,.... N — 2, и со­ответствующих игл характеристик точности приближения

Для полноты картины целесообразно рассмотреть интерполяционный (проходящий через все значения временного ряда) полином Р|\| _ 1 (t) и охарактеризовать его той же мерой приближения S2 (N — 1), равной в дан­ном случае 0. В результате будем располагать полной группой приближаю-

Надежность: коэффициенты вариации

являющиеся важнейшими показателями статистической надежности резуль­татов измерения. Величины, входящие в , означают: - дисперсию оценки i-ro коэффициента полинома порядка — дисперсию 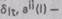i-й диагональный элемент обратной матрицы соответствующей системы нормальных уравнений.

4а. Откуда мы берем границу b0 для надежности?

Однако если со стороны "заказчика задачи" имеются требования (ограничения) к показа­телям надежности

то, установив, до какого значения (выполняются неравенства (I.4.8), можно разрешить компромисс в пользу соответствующего полинома Pk U) как "наиболее точного из допустимых по надежности"1. Если же требования оказались невыполненными для всех 1о < I < li, то следует либо принять Р|о (t) как "наилучший по надежности", либо вообще отказаться от дальней­шего решения (при данном требовании к надежности). Это и' есть конструк­тивный ответ на поставленный в начале работы вопрос: в какой степени теории следует быть близкой к исходной информации.