Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Задача линейного программирования. Геометрическая интерпретация. Симплекс метод. Двойственные задачи, основные теоремы двойственности.

Опр. Существует немало произвольного содержания задач (в основном) в экономике таких, как составление оптимального плана выпуска продукций того или иного ассортимента, оптимальное использование производственных мощностей, оптимальное распределение ресурсов, транспорта, оптимальное планирование смен, оптимальное составление рациона скота, оптимальный раскрой материала и т.д., решение которых возможно только с применением мат.аппарата. Формализация названных задач ведет к мат.модели, названной линейным программированием. Характерной особенностью такой модели является то, что целевая функция (прибыль, расходы, потребности и пр.), которая max-ся (min-ся), есть линейный функционал, а ограничение – линейное равенство или неравенство.

Функционал

(2) – общая задача линейного программирования (ОЗЛП)

F(x) – целевая функция, А- матрица условий, с- вектор стоимости, b- вектор ограничений.

Любое не отрицательное решение системы (2) является допустимым решением (допустимым планом). – условие допустимости .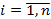

Опр. Тот из допустимых планов, который обращает называется оптимальным планом.

Конкретная ЗЛП может и не иметь оптимального плана.

Неприятности:

· Система (2) м.б. несовместной

· Система (2) совместна, но нет ни одного допустимого плана.

· Система (2) совместна, есть допустимые решения, но среди них нет оптимального.

Предположим, что система совместна и ее уравнения линейно независимы. Тогда переменных д.б. m<=n. Если m=n, то будет единственное решение.

Пусть n-m=k. Как известно из линейной алгебры какие-то n переменных(базисные) можно выразить через остальные k (свободные переменные) система имеет в этом случае бесконечное множество решений. Придавая свободным переменным произвольные значения и вычисляя соответствующие значения базисных переменных будем получать новые решения.

ЗЛП допускает геометрическую интерпретацию

Ax+By+C=0 - прямая

Ax+By+Cz+D=0 – плоскость

Симплекс-метод с искусственным базисом (M-метод)

В задачах, где нет начального базиса, создаем искусственный базис

Если в системе ограничений (3) все искусственные переменные , то перейдем к первоначальной системе ограничений (2).

Поэтому надо формировать такую целевую функцию

max-зация которой одновременно приводился бы к max нашей целевой функции f(x) и при этом все искусственные переменные обращались бы нуль.

Для любой задачи ЛП можно составить двойственную к ней задачу по следующим правилам.

1. Привести исходную задачу ЛП к стандартной форме.
2. Ввести новые переменные по числу основных ограничений исходной задачи.
3. Составить новые ограничения из новых переменных в виде линейных неравенств, знаки которых противоположны знакам неравенств исходной задачи, коэффициентами которых служат элементы транспонированной матрицы исходной задачи, а свободными членами - коэффициенты при целевой функции исходной задачи.
4. Для новых переменных написать условия неотрицательности.

В результате для исходной задачи получим следующую двойственную задачу ЛП:

Задача ЛП относительно двойственной задачи называется прямой задачей ЛП. Векторная форма задачи имеет вид:

Первая теорема двойственности (теорема о существовании решений)

А) Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение:

Х^*, у^* f₀(Х^*)=g₀(у^*)

Б) Если одна из двойственных задач не имеет смысла, то другая не имеет решения:

1) Пусть f₀(Х^*) ® ¥, тогда Q =Æ

2) Пусть g₀(у^*)® ¥, тогда R =Æ

В) Если одна из задач не имеет решения, то двойственная к ней либо не имеет смысла, либо не имеет решения.

Пункт А) следует из теоремы о критерии оптимальности прямой и двойственной задач.

Б), В) - смотри геометрическую интерпретацию практических задач.

Вторая теорема двойственности (о свойствах оптимальных решений)

Пусть имеется решение:

Х^*, у^*, если Х^*к >0, то к - ограничение. В двойственной ЗЛП при подстановке оптимального решения У^* обратится в равенство:

=c_k

Если какой-либо Х^*_L =0, то соответствующие ограничения двойственной задачи будут строго больше С_L :

>C_L

Если Y_s*>0, то =b_s

Если Y_r*=0, то < b_r

X^*_j()=0 (1)

Y^*_i(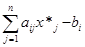)=0 (2)

Тогда теорема 2 переформулируется:

- Для того, чтобы Х^* и Y^* были оптимальными решениями, необходимо и достаточно, чтобы выполнялись условия (1) и (2).

Доказательство:

1) Необходимость

Х^*, Y^* - оптимальное решение

Доказательсть: выполняются соотношения (1) и (2)

Из критерия оптимальности следует:

f₀(Х^*)= g₀(у^*)

f₀(Х^*)= = =

Сгруппируем члены:

=

=0 (2)

£ b_i

=0 (3)

(3) - сумма неотрицательных чисел (она равна нулю, когда каждое из чисел равно нулю)

y_i* =0 ½*(-1)

Получим:

y_i* =0 ® это (2)

2) Достаточность

Для того, чтобы доказать (1) и (2) необходимо доказать, что x^* и y^* - оптимальные решения, т.е.

f₀(Х^*)= g₀(у^*)

Соотношение (1) суммируем по i, а (2) по j

, y_i*=0

=0

f₀(Х^*)= g₀(у^*)