Читайте также:
|
Рівність множин. Множини А і В рівні тоді і тільки тоді, коли кожний елемент множини А є елементом множини В, і навпаки, кожний елемент множини В є елементом множини А, тобто
А Ì В і В Ì А
Рівність множин А і В показана за допомогою діаграми Ейлера-Вена (рис.1.2).
 |
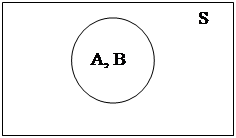Рис.1.2. Рівність множин
Об'єднання множин. Об'єднанням або сумою двох множин А и В називається множина, що складається з усіх елементів, кожний із який належить хоча б одному з даних множин (рис.1.3).
Виконуються закони:
S 1. Асоціативний
(АÈВ)ÈС=АÈ(ВÈС)=АÈВÈС.
А 2. Комутативний
АÈВ=ВÈА; АÈА=А;
Рис.1.3. Об'єднання множин АÈÆ=А;
АÈS=S; АÈВ=А, якщо В Ì А.
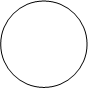
Перетинання множин. Перетинанням або добутком двох множин називається множина, що складається із усіх тих елементів, які належать обом множинам (рис 1.4). Для цієї операції праведливі комутативний і асоціативний закони. Зокрема:
S
А АÇ(ВÈС)=(АÇВ)È(АÇС).
У
| ||
 |
Рис.1.4. Перетинання множин
Дві множини А і В є взаємовиключальними, або несумісними, якщо АÇВ=Æ.
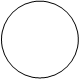
Доповнення множин. Доповненням множини А називається множина, у якій містяться всі елементи простору S, крім тих, що належать множині А. Воно позначається через `А (рис.1.5).
Справедливими будут такі
S вирази
`А А `Æ=S; `S=Æ; (A)= 
; AÈ`A=S;
A Ç`A=Æ;
Рис.1.5. Доповнення множин `A Ì`B при ВÌА;
`A =`B, якщо А=В.
Крім того, справедливі закони де - Моргана:
(АÈВ)=`А Ç`В; (АÇВ)=`А È`В.
Різниця множин. Різниця А-В множин А і В є множина, що складається з елементів множини А, які не належать множині В (рис.1.6)
A - B=A \ B=A Ç`B=A - (AÇB).
A S (читаємо “A без B”).
А-В
В
В-А
Рис.1.6. Різниця множин
З останньої діаграми виведені такі співвідношення
А - Æ = А, А - S = Æ, S - A =`A.
Вираз, де є різниця, необхідно записувати зі скобками.
Описані вище операції з множинами продемонструємо прикладом. Припустимо, що елементи простору S - натуральні числа від 1 до 6, тобто S={1, 2, 3, 4, 5, 6}, визначимо такі підмножини
А={2, 4, 6}; B={1, 2, 3, 4}; C={1, 3, 5}.
З огляду на наведені співвідношення можна записати:
(АÈВ)={1, 2, 3, 4, 6}, (BÈC)={1, 2, 3, 4, 5},
(AÈBÈC)={1, 2, 3, 4, 5, 6}=S=AÇC,
AÇB={2, 4}, BÇC={1, 3}, AÇC=Æ,
AÇBÇC=Æ,`A={1, 3, 5}=C, `B={5, 6},
`C={2, 4, 6}=A, A-B={6}, B-A={1, 3},
A-C={2, 4, 6}=A, C-A={1, 2, 5}=C,
B-C={2, 4}, C-B={5}.
Для закріплення матеріалу рекомендується проілюструвати наведені вище операції з використанням діаграм Ейлера – Вена.
Дата добавления: 2014-12-15; просмотров: 39 | Поможем написать вашу работу | Нарушение авторских прав |