Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Алгоритм однофазной модели

Рассмотренная марковская модель легко поддается автоматизации записи уравнений для последующего их анализа. Для этого запишем уравнения в матричном виде.

Для примера рассмотрим модель с N=3. Граф данной модели показан на рисунке 4.7.

Систему уравнений для нее можно получить из записи в матричном виде:

Р0´ - 3λ 3λ 0 0

Р1´ = Р0 Р1 Р2 Р3 × µ -(µ+2λ) 2λ 0 (4.10)

Р2´ 0 µ -(µ+λ) λ

Р3´ 0 0 µ -µ

Установим правило построения матрицы по графу. Пронумеруем столбцы матрицы от 0 до 3 (в общем случае до N) сверху вниз, а строки - слева направо (4.11). Матрица заполняется построчно, начиная с нулевой строки. Элементы главной диагонали записываются в последнюю очередь. Отыскиваем прямые связи из нулевой вершины в каждую другую и, при наличии, записываем в матрицу на пересечении нулевой строки и столбца с номером той вершины, с которой связана нулевая, соответствующую связи интенсивность. При отсутствии связи записываем 0. Записываем диагональный элемент из условия, что сумма элементов строки равна нулю, т.е. суммируем все элементы строки и записываем полученную сумму с противоположным знаком на место диагонального элемента текущей строки. Затем отыскиваем связи из первой вершины в каждую другую и повторяем операции до полного заполнения матрицы.

Для примера рассмотрим состояние S₀. Из S₀ в S₁ – 3λ, из S₀ в S₂ – 0, из S₀ в S₃ – 0. Сумма элементов строки равна 3λ, с противоположным знаком (-3λ) записываем диагональный элемент на пересечении строки S₀ и столбца S₀. Аналогично поступаем и с другими строками. В результате получим матрицу , элементы которой приведены в (4.4).

S₀ S₁ S₂ S₃

S₀ -3λ 3λ 0 0

S₁ µ -(µ+2λ) 2λ 0 (4.11)

S₂ 0 µ -(µ+λ) λ

S₃ 0 0 µ -µ

Используя рассмотренное правило, построим матрицу для примера, показанного на рисунке 4.5. Матрица будет иметь следующий вид:

(4.12)

Анализ матриц (4.10 – 4.12) показывает, что они имеют три диагонали – верхнюю, главную и нижнюю. Элементы нижней диагонали все одинаковые и равны µ, элементы верхней равны λ, умноженнойна коэффициент, изменяющийся при переходе к следующей строке от N (в рассматриваемом примере N=4) с шагом единица до единицы.

Зная правило формального синтеза матрицы, можно ее сформировать без рассмотрения графа марковской модели, т.е. автоматизированно. Для этого достаточно задать величины µ, λ и N и реализовать алгоритм, обеспечивающий решение по нижеприведенным формулам.

Автоматизированная запись может быть произведена на основе предварительного формирования матрицы интенсивностей l размерностью (N+1)*(N+1). Общий ее вид будет следующий:

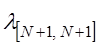= (4.9)

Элементами главной диагонали являются суммы элементов строки, взятые с противоположным знаком. Элементы верхней диагонали

l_{i-1, i} = ,

нижней диагонали

l_{i, i-1} = ,

все остальные элементы матрицы 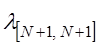равны нулю.

for i:=1 to N do for j:=1 to N do

La[i,j]:=0;

for i:=2 to N do

La[i,i-1]:=MM;

for i:=1 to N-1 do

La[i,i+1]:=(n+1-i)*Laa;

Р0´ - 3·λ 3·λ 0 0

Р1´ = Р0 Р1 Р2 Р3 × µ -(µ+2·λ) 2·λ 0

Р2´ 0 µ -(µ+λ) λ

Р3´ 0 0 µ -µ