
Читайте также:
|
Использование описанной процедуры анализа, т. е. формирование матрицы коэффициентов, решение системы уравнений и расчет по формулам (1.9) и (1.10) в. многовариантных задачах анализа, может оказаться затруднительным для задач большой размерности. Действительно, при N = 30 получим систему с числом уравнений порядка 500. Алгоритм Гаусса для такой системы имеет вычислительную сложность порядка 108 операций. Тогда время одно вариантного анализа на ЭВМ среднего быстродействия 105 оп/с составит около 103с. Так как рассмотренная модель весьма упрощенно представляет процессы решения задач с ПТК САПР, то очевидно, что нужны более эффективные методы оценки выходных параметров.
Одним из них является метод частичного укрупнения модели [З]. Идея метода заключается в том, чтобы анализ сложной по структуре модели системы осуществлять по частям, с помощью совокупности частично укрупненных моделей. В каждой из таких моделей подробно представлена некоторая часть системы, а влияние остальных частей отображается некоторым обобщенным параметром (параметром связи). В итоге получается система уравнений, описывающих изменение состояния каждой из частично укрупненных моделей.
При реализации метода частичного укрупнения (агрегирования) можно использовать принцип эквивалентности потоков. В этом случае часть системы заменяется агрегированным узлом — обслуживающим аппаратом (ОА) с очередью. Интенсивность обслуживания в таком ОА (параметр связи) зависит от числа заявок в узле. Принцип эквивалентности потоков состоит в том, что агрегированный узел при любом числе заявок в нем должен обеспечивать такой же поток во внешнюю сеть (такую же пропускную способность), как заменяемая им подсистема.
Рассмотрим применение этой идеи для анализа последней рассмотренной модели. Вместо модели, структура которой представлена на рис. 1.4, рассмотрим агрегированную модель AM1, в которой подсистема, содержащая процессор и каналы, заменена агрегированным узлом с интенсивностью обслуживания, зависящей от числа заявок. В качестве состояния в момент времени t берется число заявок в агрегированном узле. Структура модели AM1 и граф переходов изображены на рис. 1.6, а и б соответственно.
Поскольку процесс x (t) относится к классу процессов размножения-гибели, стационарное распределение записывается в явном виде:
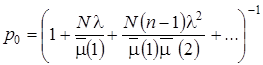 ;
;
 ;
;
....................
 ;
;
а) 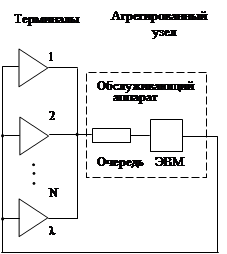
|




















|
| |||||
 | |||||
|
б) б)
 |
Рис. 1.6. Структура модели AM1 (а) и Рис. 1.7. Структура модели АМ2 (а)
граф переходов (б) и граф переходов (б)
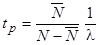 ;
;  .
.
Чтобы воспользоваться этими формулами, необходимо знать параметры связи  . Для этого используется модель АМ2, структура которой и граф переходов показаны на рис. 1.7, а, б (за состояние системы принято число заявок на процессорной фазе). Тогда интенсивности переходов в графе
. Для этого используется модель АМ2, структура которой и граф переходов показаны на рис. 1.7, а, б (за состояние системы принято число заявок на процессорной фазе). Тогда интенсивности переходов в графе
ni = n min { M, n-i }, i =  .
.
Стационарное распределение представляется соотношениями:
 ;
;  ;
;
Тогда параметры связи
 .
.
1) для п от 1 до N по формулам (1.12), (1.13), (1.14) определяются  ;
;
2) по формулам (1.11) рассчитываются характеристики системы.
Процедуру частичного укрупнения моделей можно использовать многократно, при этом анализируемая модель последовательно упрощается.
Лекція № 11. ЗАРУБІЖНИЙ ДОСВІД СОЦІАЛЬНОГО СТРАХУВАННЯ
Ключові питання:
1. Огляд систем соціального страхування зарубіжних країн.
2. Типологія світових моделей соціального захисту.
3. Типологія національних систем організації соціального страхування.
4. Стратегія корпоративної соціальної відповідальності – інноваційна ініціатива Європейської комісії у сфері соціального страхування.
5. Проблеми розвитку системи соціального страхування за кордоном та в Україні.
Дата добавления: 2014-12-15; просмотров: 108 | Поможем написать вашу работу | Нарушение авторских прав |