Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Систематические линейные блочные коды

Систематический линейный блочный код (systematic linear block code) (n, k) — это такое отображение n-мерного вектора сообщения в n-мерное кодовое слово, что часть генерируемой последовательности совмещается с k символами сообщения. Остальные бит – это биты четности. Матрица генератора систематического линейного блочного кода имеет следующий вид.

(6.27)

Здесь Р – массив четности, входящий в матрицу генератора, pij = (0 или 1), а Ik – единичная матрица размерностью k x k (у которой диагональные элементы равны 1, а все остальные – 0). Заметим, что при использовании этого систематического генератора процесс кодирования еще больше упрощается, поскольку нет необходимости хранить ту часть массива, где находится единичная матрица. Объединяя выражения (6.26) и (6.27), можно представить каждое кодовое слово в следующем виде.

где

Для данного k-кортежа сообщения

и k-кортежа кодовых векторов

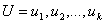
систематический кодовый вектор можно записать в следующем виде.

(6.28)

где

(6.29)

Систематические кодовые слова иногда записываются так, чтобы биты сообщения занимали левую часть кодового слова, а биты четности — правую. Такая перестановка не влияет на свойства кода, связанные с процедурами обнаружения и исправления ошибок, поэтому далее рассматриваться не будет.

Для кода (6,3), рассмотренного в разделе 6.4.3, кодовое слово выглядит следующим образом.

(6.30)

(6.31)

Выражение (6.31) позволяет получить некоторое представление о структуре линейных блочных кодов. Видно, что избыточные биты имеют разное происхождение. Первый бит четности является суммой первого и третьего битов сообщения; второй бит четности — это сумма первого и второго битов сообщения; а третий бит четности — сумма второго и третьего битов сообщения. Интуитивно понятно, что, по сравнению с контролем четности методом дублирования разряда или с помощью одного бита четности, описанная структура может предоставлять более широкие возможности обнаружения и исправления ошибок.