
Читайте также:
|
ДОМАШНЕЕ ЗАДАНИЕ № 1 «Высказывания и множества»
1. Известно, что импликация р 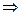 q истинна, а эквиваленция р
q истинна, а эквиваленция р  q ложна. Что можно сказать о значениях эквиваленции q
q ложна. Что можно сказать о значениях эквиваленции q  p u импликации q
p u импликации q 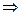 p.
p.
2.Определить значения высказываний р  (q
(q  s) и р
s) и р  q
q 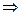 s, если р = Л, q = Л, s = И.
s, если р = Л, q = Л, s = И.
3. Построитьтаблицы истинности для сложного высказывания С=( В)
В)  А:
А:
4.Найти истинностные значения р и q, при которых выполняется равенство р  q =
q = 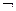 р.
р.
5. Заданы множества А = 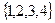 и В =
и В =  , тогда для них верным утверждением будет….
, тогда для них верным утверждением будет….
| А | Множество В есть подмножество А |
| В | Множество А есть подмножество В |
| С | Множества А и В равны |
| Д | Множества А и В не имеют одинаковых элементов |
6.Вставьте между множествами символ Î или Í, чтобы получилось истинное высказывание: {a} … {a, {a, б}}
7.Найдите AÈ B, A Ç B, A \ B, B \ A, 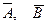 , если: A = { x | x £ 5 }; B = { x | 3< x < 7}, U = R
, если: A = { x | x £ 5 }; B = { x | 3< x < 7}, U = R
ДОМАШНЕЕ ЗАДАНИЕ № 2 «Комбинаторика»
1) В нашем распоряжении есть три флага. На флагштоке поднимается сигнал, содержащий 1, 2 или 3 флага. Сколько различных сигналов можно поднять на флагштоке, если сигналы, поданные одними и теми же флагами, поднятыми в различном порядке, считать различными?
2) Для проведения экзамена создается комиссия из двух преподавателей. Сколько различных комиссий можно создать из пяти преподавателей?
3) Для дежурства в классе в течение недели (кроме воскресенья) выделены 6 учащихся. Сколькими способами можно установить очередность дежурств, если каждый учащийся дежурит один раз?
4) В магазине «Всё для чая» есть: а) 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем? б) добавим ещё 4 чайные ложки. Сколькими способами можно получить комплект из чашки, блюдца и ложки? в) 5 чашек, 3 блюдца, 4 чайные ложки. Сколькими способами можно купить два предмета с разными названиями?
5) Из букв слова «поле» составить всевозможные трехбуквенные слова (включая бессмысленные).
6) Сколько различных четырехзначных чисел можно составить из цифр: а) 2, 3, 4, 5; б) 2, 3, 4, 5, 6, 7; в) 2, 3, 4, 5, 6, 7, 0.
7) В седьмом классе изучаются 14 предметов. Сколькими способами можно составить расписание занятий на субботу, если в этот день недели должно быть пять различных уроков?
8) Решите уравнение: а) 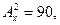 б)
б)  , в)
, в) 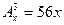 .
.
9) Скольким способами можно рассадить 12 человек за круглым столом?
ДОМАШНЕЕ ЗАДАНИЕ № 3 «Вероятность»
1.В урне 2 белых и 4 черных шара. Опыт состоит в выборе только одного шара. Событие А – «Вынули белый шар», событие В – «Вынули черный шар». Тогда для этих событий неверным будет утверждение:
| Вероятность события В больше вероятности события А | |
| События А и В несовместны | |
| События А и В равновероятны | |
Вероятность события В равна 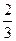
|
2. Вероятность наступления некоторого события не может быть равна а) 1; в) 0,4; с) -0,7; д) 0.
3. Игральный кубик бросают один раз. Найти вероятность того, что на верхней грани выпадет число очков, меньше, чем шесть, но больше 3.
4. В ящике лежат 20 одинаковых на ощупь шаров. Из них 12 белых и 8 черных. Наугад вынимают один шар. Какова вероятность того, что он окажется белым?
5. Первый студент не сдаст сессию с вероятностью 0,2, а второй с вероятностью – 0,3. Чему равна вероятность того, что оба они сдадут сессию?
6. Вероятность поражения цели первым стрелком (событие А) равна 0,9, а вероятность поражения цели вторым стрелком (событие В) равна 0,8. Какова вероятность того, что цель будет поражена хотя бы одним стрелком?
7. В урне находятся 2 белых, 3 красных и 5 синих одинаковых по размеру шаров. Какова вероятность, что шар, случайным образом извлеченный из урны, будет цветным (не белым)?
8. В первой урне 1 белых и 9 черных шаров. Во второй урне 3 черных и 7 белых шаров. Из наудачу взятой урны вынули один шар. Чему равна вероятность того, что этот шар окажется черным?
ДОМАШНЕЕ ЗАДАНИЕ № 4 «Случайные величины»
1. Средняя выборочная вариационного ряда 1, 2, 5, 5, 5 равна: А. 6 В. 3,6 С. 3,1 D. 5
2. Дискретная случайная величина Х имеет закон распределения вероятностей
| Х | ||
| Р | 0,7 | 0,3 |
Математическое ожидание М(Х) этой случайной величины равно:
А. 1,3 В. 1 С. 1,7 D. 3
3. В результате 10 опытов получена следующая выборка: 2, 2, 2, 3, 3, 4, 4, 4, 6, 6. Найти закон ее распределения.
4. Для вариационного ряда 1, 2, 5, 3, 2 вычислить: 1) Выборочное среднее 2) Выборочную дисперсию 3) Выборочное среднее квадратическое отклонение
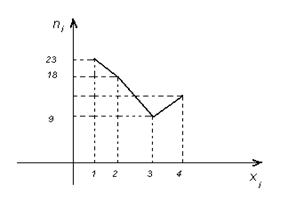 5. Из генеральной совокупности извлечена выборка объема п=65, полигон частот которой имеет вид:
5. Из генеральной совокупности извлечена выборка объема п=65, полигон частот которой имеет вид:
Число вариант х=4 в выборке равно
А. 12
В. 14
С. 15
D. 13
ДОМАШНЕЕ ЗАДАНИЕ № 5 «Системы линейных уравнений»
1. Решить систему линейных уравнений методом подстановки 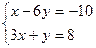
2. Решить систему линейных уравнений (1) с помощью правила Крамера, (2) с помощью метода Гаусса.
(1) 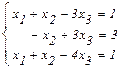
(2) 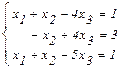
05-04/02
Методичні вказівки
до виконання практичних занять
з дисципліни «Метрологія і стандартизація»
студентами за напрямом підготовки 6.080101 «Геодезія, картографія та землеустрій» денної та заочної форм навчання
Рекомендовано методичною
комісією за напрямом підготовки
«Геодезія, картографія та землеустрій»
Протокол № 1 від 05.09.2013 р.
Рівне – 2013
Методичні вказівки до виконання практичних занять з дисципліни «Метрологія і стандартизація» студентами за напрямом підготовки 6.080101 «Геодезія, картографія та землеустрій» денної та заочної форм навчання / І.М. Бялик. – Рівне: НУВГП, 2013. – 30 ст.
Упорядник: Бялик Ігор Миколайович, к.т.н., доцент кафедри геодезії та геоінформатики.
Відповідальний за випуск: Янчук Р.М., к.т.н. доцент, в.о. завідувача кафедри геодезії та геоінформатики.
© Бялик І.М., 2013
© НУВГП, 2013
Зміст
| Передмова ………………………...……………...……………….. | |
| Практична робота №1 Одиниці вимірювання різних систем та їх взаємне перетворення…………...………………………………. | |
| Практична робота №2 Загальна характеристика геодезичних приладів, як засобів вимірювальної техніки………………...…....... | |
| Практична робота №3 Організація метрологічного забезпечення геодезичних приладів………………..…………………. | |
| Практична робота №4 Організація та проведення геодезичних вимірювань………………………………...……………… | |
| Практична робота №5 Основи теорії похибок вимірювань та оцінка точності геодезичних вимірювань………………………….. | |
| Практична робота №6 Державні стандарти України (ДСТУ) та інші нормативно-правові документи в галузі метрології, геодезії та землевпорядкування ……………………………………… | |
| Практична робота №7 Ліцензування у галузі землевпорядних робіт та оцінки землі ………………................................................. | |
| Рекомендована література……………………………………… |
Дата добавления: 2014-12-15; просмотров: 180 | Поможем написать вашу работу | Нарушение авторских прав |