
Читайте также:
|
Решить задачу ЛП это значит найти такие значения переменных, которые удовлетворяют всем ограничениям, а ЦФ достигает искомого экстремума.
Геометрическая интерпретация задач ЛП позволяет наглядно представить их структуру и выявить их особенности. Задачу ЛП с двумя переменными всегда можно решить графически. Однако в трехмерном пространстве такое решение существенно усложняется, а в пространстве размерность которого больше трех, графическое решение, вообще говоря, невозможно.
Рассмотрим математическую модель общей задачи ЛП в стандартной форме:
Z=c1x1+c2x2 – max
a11x1 + a12x2 ≤ b1
a21x1 + a22x2 ≤ b2
– – – – – –
am1x1 + am2x2 ≤ bm
x1, x2 ≥ 0
Дадим геометрическую интерпретацию элементов этой задачи. Выполнить геометрическую интерпретацию задачи ЛП означает поставить в соответствие каждой части математической модели задачи (целевой функции, системе ограничений, условию неотрицательности) геометрические образы.
Геометрическим образом линейного уравнения с двумя неизвестными явл. прямая
 3x1+2x2 =6
3x1+2x2 =6
 |
Геометрическим образом линейного неравенства явл. одна из 2-хполуплоскостей, на которые соответствующая прямая делит всю плоскость x1Ox2.
Чтобы определить координаты точек какой полуплоскости, удовлетворяют заданному неравенству, нужно в левую часть неравенства подставить координаты какой-нибудь точки, лежащей в одной из полуплоскостей. Удобно взять координаты начала – т. (0,0). Если координаты взятой точки удовлетворяют неравенству, то ему будут удовлетворять координаты всех точек, расположенных в той же полуплоскости, что и взятая точка.
Рассмотрим условие неотрицательности переменных. x1,x2 ≥ 0. Геометрическим образом условия неотрицательности переменных явл. 1-я четверть.
Свойства решений задачи ЛП тесно связаны со свойствами выпуклых множеств.
Полуплоскость является выпуклым множеством.
Пусть на плоскости Х1ОХ2 заданы две точки: А1 и А2.
 |
Выпуклым множеством называется множество, которое вместе с любыми своими точками А1 и А2 содержит и все точки А отрезка [А1;А2]. Т.е. точки  , где 0≤ λ ≤1,
, где 0≤ λ ≤1,
Иногда это свойство записывают иначе:
 , (1)
, (1)
где λ1 ≥ 0 и λ2 ≥ 0; λ1+λ2 =1. (2)
Т.А, для которой выполняется условие (1) и (2) называется выпуклой линейной комбинацией точек А1 и А2. При λ1=1 и λ2 =0 т.А совпадает с концом отрезка А1. При λ1=0 и λ2 =1 т.А совпадаетс концом отрезка А2.
Соотношения (1) и (2) верны и для n точек А1,А2,…,Аn
Т.А явл.их выпуклой лин. Комбинацией, если выполняются условия:
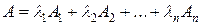
где λj ≥ 0 (j=1,1,…,n); 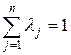
Точки А1 и А2 наз. угловыми или крайними точками отрезка А1 А2. Из определения линейной выпуклой комбинации точек очевидно, что угловая точка не может быть представлена как выпуклая линейная комбинация двух других точек отрезка.
Т.е. угловыми точками выпуклового множества наз. точки, не являющиеся выпуклой комбинацией двух произвольных точек множества.
Например. Треугольник, вершины являются угловыми точками.
Прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют. Пересечение любого числа выпуклых множеств является выпуклым множеством. Отсюда следует, что область допустимых решений задачи есть выпуклое множество.
 |  | ||
Геометрическим образом системы неравенств (или структурных ограничений) и условия неотрицательности, явл. общая часть полуплоскостей (многоугольник) расположенная в 1-ой четверти.
 |




 X2
X2
 |
 X1
X1
Выпуклый многоугольник ABC наз. областью допустимых решений (ОДР) или многоугольником ограничений. Внутри этого многоугольника и на границах находятся решения, удовлетворяющие ограничениям задачи.
Рассмотрим геометрический образ ЦФ.
Z=c1x1+c2x2 – max
Пусть ОДР – непустое множество. Выберем произвольное значение целевой функции Z=const= D. (Зададим произвольное значение D). Получим:
c1x1+c2x2 = D – (1) – это уравнение прямой линии.
Очевидно, что, если считать D -параметром, и задавая D различные значения, получим уравнения семейства параллельных прямых, называемых линиями уровняцелевой функции (линиями постоянного значения).
Также очевидно, что при перемещении в какую-то одну сторону будем получать большие значения ЦФ, а при перемещении в противоположную – меньшие.
Встает вопрос: как определить направление возрастания (убывания) ЦФ?
Существует два способа:
1. В левую часть ур-я (1) подставить координаты какой-нибудь точки, не лежащей на этой прямой (удобно брать т.(0,0))
2. Найдем частные производные по x1 и x2 .
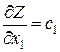 (2)
(2)
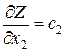 (3)
(3)
Частная производная (2) и (3) функции показывает скорость ее возрастания вдоль данной оси. Следовательно, с1 и с2 – скорости возрастания ЦФ Z вдоль осей Оx1 и Ox2.
Вектор С=(с1 , с2) называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:

Вектор «–С» – указывает направление наискорейшего убывания целевой функции. Его наз. антиградиентом.
Вектор С=(с1 ,с2) перпендикулярен к прямым Z=const семейства Z=c1x1+c2x2 (линиям уровня целевой функции Z).
В теории ЛП доказывается, что оптимальный план задачи ЛП достигается по крайней мере в одной из вершин ОДР.
Общие и частные случаи вида ОДР.







 ОДР - выпуклый замкнутый многоугольник
ОДР - выпуклый замкнутый многоугольник
ABCDEF. Линия Уровня и ОДР имеют одну
общую точку.








 ОДР - выпуклый замкнутый многоугольник
ОДР - выпуклый замкнутый многоугольник
ABCDEF. Линия Уровня проходит через
сторону BC и имеет бесконечное множество
оптимальных планов. Их еще наз.
альтернативными планами. Разные планы
с одинаковыми значениями ЦФ





 ОДР – выпуклый незамкнутый.
ОДР – выпуклый незамкнутый.
многоугольник ABC
Оптимальный план существует и достигается в т.С





 ОДР – выпуклый незамкнутый
ОДР – выпуклый незамкнутый
многоугольник ABC
Целевая функция не ограниченна. Сколько бы
 ее ни передвигали, она не может занять своего
ее ни передвигали, она не может занять своего
 разрешающего положения. ЦФ неограничена.
разрешающего положения. ЦФ неограничена.
 Z=+∞
Z=+∞



 ОДР – выпуклый незамкнутый
ОДР – выпуклый незамкнутый
многоугольник ABC

 Целевая функция не ограниченна. Сколько бы
Целевая функция не ограниченна. Сколько бы
 ее ни передвигали, она не может занять своего
ее ни передвигали, она не может занять своего
 разрешающего положения. ЦФ неограничена.
разрешающего положения. ЦФ неограничена.
 Z= + ∞; Z= – ∞
Z= + ∞; Z= – ∞
 | ||
 |
 ОДР – состоит из единственной точки, где
ОДР – состоит из единственной точки, где

 ЦФ достигает одновременно и максимума
ЦФ достигает одновременно и максимума
 и минимума
и минимума



 ОДР – пустое множество. Т.е. система
ОДР – пустое множество. Т.е. система
 ограничений противоречива, несовместна.
ограничений противоречива, несовместна.
Задача наз. недопустимой, у нее нет ни одного
допустимого решения.

Порядок графического способа решения задачи ЛП
Из геометрической интерпретации задачи ЛП вытекает следующий порядок ее графического способа решения задачи.
1. Строим область допустимых решений (ОДР) с учетом ограничений задачи.
2. Строим произвольную линию уровня Z=Z0. Проще построить линию Z=0.
3. Строим вектор наискорейшего возрастания ЦФ. Вектор-градиент С=(с1, с2).
4. При решении задачи на MAX перемещаем линию уровня ЦФ Z=0 в направлении вектора-градиента С=(с1, с2), так, чтобы она касалась ОДР в ее крайнем положении (крайней точке). В случае решения задачи на MIN линию уровня ЦФ передвигают в противоположном (антиградиентном) направлении.
Дата добавления: 2014-12-15; просмотров: 261 | Поможем написать вашу работу | Нарушение авторских прав |