Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Метод вариации произвольных постоянных. Для линейного неоднородного уравнения первого порядка с постоянными коэффициентами.

Метод вариации произвольных постоянных применяется для решения неоднородных дифференциальных уравнений.
. На первом этапе необходимо решить вспомогательное уравнение: .
Перед нами уравнение с разделяющимися переменными. Находим общее решение вспомогательного уравнения.
На втором шаге заменим константу 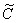некоторой пока ещё неизвестной функцией , которая зависит от «икс».
Отсюда и название метода – варьируем константу 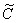. нам предстоит сейчас найти.
В исходном неоднородном уравнении проведём замену константы на u. Найдём производную y’. Подставим y и y’ в изменённое исходное уравнение. Два слагаемых в левой части сокращаются. В результате замены получено уравнение с разделяющимися переменными. Разделяем переменные и интегрируем. К найденной функции приплюсовываем «нормальную» константу . На заключительном этапе вспоминаем про нашу замену.