Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Метод характеристического уравнения (метод Эйлера).

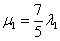
1) Смотрим на систему уравнений и составляем определитель второго порядка из коэффициентов k,m,l,n.
2) Составим характеристическое уравнение, для этого из каждого числа, которое располагается на главной диагонали, вычитаем некоторый параметр .
3) Раскрываем определитель и находим корни квадратного уравнения.
4) Если характеристическое уравнение имеет два различных действительных корня, то общее решение системы дифференциальных уравнений имеет вид:

Коэффициенты в показателях экспонент нам уже известны, осталось найти коэффициенты .
5)Подставим первый полученный корень в характеристическое уравнение.
6) Из чисел определителя составим систему двух линейных уравнений с двумя неизвестными типа:

7) Из обоих уравнений следует одно и то же равенство:
8) Теперь нужно подобрать наименьшее значение , такое, чтобы значение было целым.
9)Аналогично рассматриваем второй корень.
10) Подставляем найденные коэффициенты в (4) – общее решение.