Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Метод вариации произвольных постоянных для линейного неоднородного уравнения второго порядка с постоянными коэффициентами.

Вспоминаем, что линейное неоднородное уравнение второго порядка с постоянными коэффициентами имеет вид:

Пример 4

Найти общее решение дифференциального уравнения второго порядка

Решение: В правой части данного уравнения находится дробь, поэтому сразу можно сказать, что метод подбора частного решения не прокатывает. Используем метод вариации произвольных постоянных.

Ничто не предвещает грозы, начало решения совершенно обычное:

Найдем общее решение соответствующего однородного уравнения:

Составим и решим характеристическое уравнение:


– получены сопряженные комплексные корни, поэтому общее решение:

Обратите внимание на запись общего решения – если есть скобки, то их раскрываем.

Теперь проделываем практически тот же трюк, что и для уравнения первого порядка: варьируем константы , заменяя их неизвестными функциями 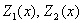. То есть, общее решение неоднородного уравнения будем искать в виде:

, где 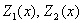– пока ещё неизвестные функции.

Далее необходимо решить систему двух уравнений с двумя неизвестными:

Похоже на свалку бытовых отходов, но сейчас всё рассортируем.

В качестве неизвестных выступают производные функций . Наша цель – найти производные , причем найденные производные должны удовлетворять и первому и второму уравнению системы.

Откуда берутся «игреки»? Их приносит аист. Смотрим на полученное ранее общее решение и записываем:

,

Найдем производные:

С левыми частями разобрались. Что справа?

– это правая часть исходного уравнения, в данном случае:

Коэффициент – это коэффициент при второй производной:

На практике почти всегда , и наш пример не исключение.

Всё прояснилось, теперь можно составить систему:

Систему обычно решают по формулам Крамера, используя стандартный алгоритм. Единственное отличие состоит в том, что вместо чисел у нас функции.

Найдем главный определитель системы:

Итак: , значит, система имеет единственное решение.

Едем дальше:

Находим производную:

Но это еще не всё, пока мы нашли только производную.
Сама функция восстанавливается интегрированием:

Здесь добавляем «нормальную» константу

Разбираемся со второй функцией:

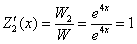
Здесь добавляем «нормальную» константу

На заключительном этапе решения вспоминаем, в каком виде мы искали общее решение неоднородного уравнения? В таком:

Нужные функции только что найдены!

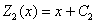
Осталось выполнить подстановку и записать ответ:

Ответ: общее решение: .