Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Однородные дифференциальные уравнения первого порядка.

В исходное уравнение вместо подставляем , вместо подставляем , производную не трогаем. Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.
Абсолютно все однородные уравнения можно решить с помощью одной-единственной стандартной замены: функцию «игрек» необходимо заменитьпроизведением некоторой функции (тоже зависящей от «икс») и «икса»: . . После данной замены и проведенных упрощений мы гарантировано получим уравнение с разделяющимися переменными. Для любого однородного уравнения нужно провести одну и ту же замену: строго и, соответственно, строго . Где производная равна: .

Линейные дифференциальные уравнения первого порядка. Метод Бернулли.

Если переменные разделить не удалось, и уравнение однородным не является, то в 90% случаев перед вами как раз линейное неоднородное уравнение первого порядка. Линейное уравнение первого порядка в стандартной записи имеет вид:
1) первая производная - ; 2) произведение , где – функция, а 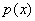– выражение, зависящее только от «икс»; 3) выражение , тоже зависящее только от«икс». В частности, может быть константой. Выражение 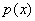тоже может быть некоторой константой.
Рядом с производной может находиться множитель , зависящий только от «икс».
Решается одной-единственной заменой: 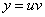, где и – некоторые, пока ещё неизвестные функции, зависящие от «икс».

После подстановки смотрим на два слагаемых, которые располагаются вот на этих местах:
. У них нужно вынести за скобки всё, что можно вынести. В данном случае:
. Теперь нужно составить систему уравнений. Приравниваем к нулю то, что находится в скобках: 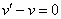. Если 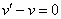, тогда из нашего уравнения получаем . Уравнения записываем в систему: . Сначала из первого уравнения находим функцию . Константу на данном этапе мы не приписываем. Далее подставляем найденную функцию во второе уравнение системы : . Из второго уравнения находим функцию . Функция найдена. А вот здесь уже добавляем константу .