
Читайте также:
|
Сложение векторов  и
и 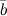 осуществляется по правилу треугольника.
осуществляется по правилу треугольника.
Суммой  двух векторов
двух векторов  и
и 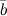 называют такой третий вектор
называют такой третий вектор  , начало которого совпадает с началом
, начало которого совпадает с началом  , а конец - с концом
, а конец - с концом 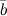 при условии, что конец вектора
при условии, что конец вектора  и начало вектора
и начало вектора 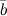 совпадают (рис. 1).
совпадают (рис. 1).

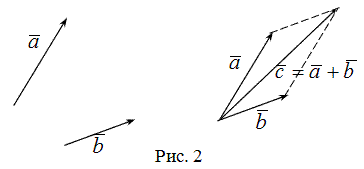
Для сложения векторов применяется также правило параллелограмма.
Правило параллелограмма - если два неколлинеарных вектора  и
и 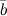 привести к общему началу, то вектор
привести к общему началу, то вектор  совпадает с диагональю параллелограмма, построенного на векторах
совпадает с диагональю параллелограмма, построенного на векторах  и
и 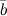 (рис. 2). Причем начало вектора
(рис. 2). Причем начало вектора  совпадает с началом заданных векторов.
совпадает с началом заданных векторов.
Вектор  называется противоположным вектором к вектору
называется противоположным вектором к вектору  , если он коллинеарен вектору
, если он коллинеарен вектору  , равен ему по длине, но направлен в противоположную сторону вектору
, равен ему по длине, но направлен в противоположную сторону вектору  .
.
Операция сложения векторов обладает следующими свойствами:
1.  - коммутативность
- коммутативность
2.  - ассоциативность
- ассоциативность
3. 
4. 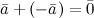
Разностью  векторов
векторов  и
и 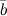 называется вектор
называется вектор  такой, что выполняется условие:
такой, что выполняется условие: 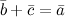 (рис. 3).
(рис. 3).
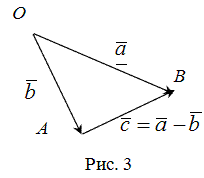
Дата добавления: 2015-02-16; просмотров: 413 | Поможем написать вашу работу | Нарушение авторских прав |