Читайте также:
|
Произведением 
вектора 
на число 
называется вектор 
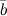, удовлетворяющий условиям:
1. 
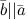
2. 
3. 
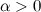, если 
, 
, если 
Свойства умножения вектора на число:
1. 
2. 
3. 
4. 
5. 
6. 
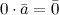
Здесь и 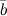- произвольные векторы, , 
- произвольные числа.
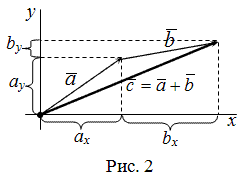
Сумма двух векторов, заданных координатами
Пусть заданы 
и 
, тогда вектор 
имеет координаты 
(рис. 2).
Определение
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.
Пример
Задание. Заданы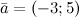 
и 
. Найти координаты вектора
Решение. 
Умножение вектора на число
Если задан , то тогда вектор 
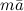имеет координаты 
, здесь 
- некоторое число (рис. 3).
Определение
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Пример
Задание. Вектор 
. Найти координаты вектора 
Решение. 
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки 
и 
. Тогда координаты вектора 
находятся по формулам (рис. 4):
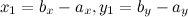
Дата добавления: 2015-02-16; просмотров: 112 | Поможем написать вашу работу | Нарушение авторских прав |