Использование координат векторов (точек) при решении математических задач(простейшие задачи в координатах).

Билет № 16

1.Функция y=sin(x), ее свойства и график.

Область определения – множество всех действительных чисел.

Область значение – отрезок [-1; 1]

Функция периодична. Основной период равен 2π.

Функция нечетная.

Функция возрастает на промежутках и убывает на промежутке , где n принадлежит множеству целых чисел.

Первообразная функции. Таблица первообразных элементарных функций. Основное свойство первообразной.

Функцию y = F(x) называют первообразной функции y = f(x) на промежутке х, если для любого х из Х выполняется равенство F’(x) = f(x).

Если F(x) первообразная для функции y = f’(x) на промежутке х, то у функции y = f(x) бесконечно много первообразных и все эти первообразные имеют вид F(x) + C, где С – любое действительное число.

Операцию отыскания первообразной называются операцией обратной дифференцированию.

Функция	Первообразная	Функция	Первообразная
k	kx + C	cos x	sin x
xr			-ctg x
	ln x + C		tg x
ex	ex + C		arssin x
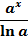
	Ax		arctg x
sin x	- cos x

Свойства первообразных:

1. Первообразная суммы равная сумме первообразных.

F (x) + H (x) = f (x) + h (x)

2. Постоянный множитель можно вынести за знак первообразной.

f (kx) = kF(x)

3. Если F(x) первообразная для f(x), а k и b – постоянные, причем k ≠ 0, то первообразная для f(kx+b).

3.Исследовать функцию и построить ее график.