Читайте также:
|
Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.
Пример
Задание. Найти скалярное произведение векторов 
и 
Решение. Скалярное произведение
Длина вектора
Длина вектора 
, заданного своими координатами, находится по формуле:
Определение
Длина (модуль) вектора, координаты которого известны, равен корню квадратному из суммы квадратов координат.
Пример
Задание. Найти длину вектора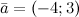 
Решение. Используя формулу, получаем:
47.
Векторным произведением ненулевых векторов 
и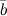 
называется вектор 
, обозначаемый символом 
или 
, длина которого 
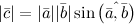(рис. 1).
Свойства векторного произведения:
1° 
, тогда и только тогда, когда 
2° 
3° Модуль векторного произведения 
равен площади параллелограмма, построенного на заданных векторах и 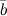(рис. 2), т.е.
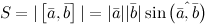
4°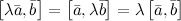 
5° 
Если векторы заданы своими координатами , 
, то векторное произведение находится по формуле:
Пример
Задание. Найти векторное произведение векторов 
и 
Решение. Составляем определитель и вычисляем его:
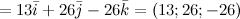
Дата добавления: 2015-02-16; просмотров: 71 | Поможем написать вашу работу | Нарушение авторских прав |