Читайте также:
|
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Пример
Задание. Найти координаты вектора 
, если 
Решение. 
Скалярным произведением двух ненулевых векторов 
и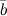 
называется число, равное произведению длин этих векторов на косинус угла между ними:
Пример
Задание. Вычислить скалярное произведение векторов и 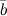, если их длины соответственно равны 2 и 3, а угол между ними 60°.
Решение. Так как из условия 
, 
, а 
, то
Если хотя бы один из векторов или 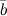равен нулевому вектору, то 
.
Свойства скалярного произведения:
1° 
- симметричность.
2° 
. Обозначается 
и называется скалярный квадрат.
3° Если 
, то 
4° Если и 
и 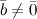, то 
. Верно и обратное утверждение.
5°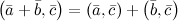 
6° 
7° 
46.
Если векторы и 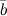заданы своими координатами: 
, 
, то их скалярное произведение вычисляется по формуле:
Дата добавления: 2015-02-16; просмотров: 77 | Поможем написать вашу работу | Нарушение авторских прав |