
Читайте также:
|
1. Суммой матриц А и В называют такую матрицу, элементы которой равны сумме соответствующих элементов матриц А и В.
Складывать можно только матрицы, имеющие одинаковое строение: или прямоугольные типа m x n, или квадратные порядка n.
Пусть 

Тогда сумма матриц С=А+В имеет вид:
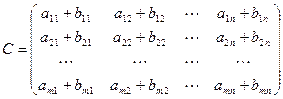
В частности, А-В=А+(-В)
2. Произведением матрицы А на число k называется такая матрица kA, каждый элемент которой равен kaij, т.е. умножение матрицы на число сводится к умножению на это число всех элементов матрицы.
Если  , то
, то 
Так как сумма (разность) матриц и умножение матрицы на число сводится к сложению (вычитанию) и умножению чисел, то эти операции подчиняются основным законам сложения и умножения:
1) A + B = B + A (коммутативность сложения матриц);
2) (A + B) + C = A + (B + C) (ассоциативность сложения матриц);
3) A + O = A;
4) A + (–A) = O;
5) α⋅(βA) = (α⋅β)A (ассоциативность относительно умножения чисел);
6) (α+β)A = αA+ βA (дистрибутивность умножения на матрицу относительно сложения чисел);
7) α(A + B)= αA+ αB (дистрибутивность умножения на число относительно сложения матриц);
8) 1⋅A = A.
Пример:
Даны матрицы А = 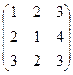 ; B =
; B =  .
.
Найти 2А + В.
Решение
2А =  ,
,
2А + В = 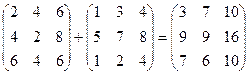 .
.
Дата добавления: 2015-02-16; просмотров: 67 | Поможем написать вашу работу | Нарушение авторских прав |