Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Методы исключения (уменьшения) случайных, систематических и грубых погрешностей

1. Случайные погрешности.

Случайные погрешности формируются под влиянием многочисленных факторов, учет которых практически неосуществим, поэтому исключить эти погрешности из результатов измерения невозможно.

2. Исключение систематической погрешности.

Осуществляют в тех случаях, когда на более ранних стадиях измерительного процесса указанные погрешности не удалось уменьшить до уровня незначительных случайных составляющих. Поскольку случайная составляющая измерения определяется значением , то при известной малой величине этого значения, требование к величине неисключенного остатка систематической погрешности можно записать в виде:

3. Грубые погрешности можно рассматривать как результаты наблюдений, не принадлежащие исследуемой генеральной совокупности и, следовательно, они должны быть исключены из дальнейшей статистической обработки. Соответствующая операция получила название цензурирования выборки.

Наиболее наглядный способ цензурирования предполагает построение гистограмм распределения результатов наблюдений. При этом, если часть экспериментальных данных будет иметь отличное от остальных распределение, то, ясно, что она не принадлежит генеральной совокупности наблюдения.

Правило трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического результата измерений не превосходит утроенной средней квадратической ошибки этого среднего значения.

Основываясь на этом правиле, можно сформулировать простейший способ выявления промахов. Из анализируемой выборки удаляют сомнительные отсчеты. Затем по оставшимся в выборке данным вычисляют эмпирический стандарт S и все значения для которых признают промахами, исключая их из дальнейшей выборки.

Еще один способ обнаружения результатов наблюдений, содержащих грубые погрешности, заключается в следующем. Все полученные результаты представляют в виде упорядоченного ряда . Если крайние члены, являющиеся наибольшим и наименьшим результатами, значительно отстоят от ближайших членов, то это дает основание для проверки их на наличие грубых погрешностей. Такую проверку осуществляют на основе сравнения сомнительного (выскакивающего) значения с остальными результатами наблюдений. Для этого вычисляют дробь:

– среднее арифметическое и СКО экспериментальных данных.

Затем задают уровень значимости 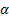, т.е. вероятность того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений. 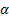выбирают из ряда 1, 2, 5, 10%. Далее сравнивают вычисленное значение с теоретическим значением -процентной точки наибольшего по абсолютному значению нормированного выборочного отклонения.

Если при числе n измерений , то экспериментальное данное подлежит исключению, как содержащее грубую погрешность.

Основные понятия вероятностной теории погрешности: случайная величина, генеральная совокупность, выборка и их характеристики

Случайной, называют величину, которая в результате опыта принимает то или иное значение.

Различают дискретные и непрерывные случайные величины.

Дискретная случайная величина может принимать лишь счетное множество значений
с вероятностями . При этом все возможные значения случайно величины образуют полную группу событий, для которых

Наиболее полной характеристикой дискретной величины является ее распределение вероятностей. Оно представляет собой пересечения всех возможных значений случайной величины с указанием вероятностей 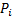этих значений.

Непрерывная случайная величина может принимать любое значение из конечного или бесконечного интервала. Поскольку значения могут отличаться друг от друга на сколь угодно малую величину, то вероятность каждого из них также бесконечно мала.

Генеральная совокупность – полное множество всех возможных значений случайной величины (результатов отдельных измерений).

Однако из-за ряда (экономических, технических и др.) число экспериментально полученных значений изучаемой величины всегда ограничено некоторым действительным множеством, выборкой. Выборка, являясь лишь одним из вариантов наблюденных значений физической величины, не содержит точной информации об ее распределении. Тем не менее, она позволяет получить оценки числовых характеристик плотности и функции распределения, что является предпосылкой выборочного метода.

Наиболее важным принципом в применении этого метода является обеспечение равно вероятности всем элементам, образующим генеральную совокупность, быть выбранными. Реализация этого принципа позволяет получить так называемую репрезентативную выборку, характеристики которой при увеличении числа составляющих ее элементов стремятся к характеристикам генеральной совокупности.