Читайте также:
|
Регреессия — зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин.
Корреляция — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Пусть имеется достаточно оснований полагать регрессию линейной. Тогда уравнение выборочной линии регрессии будет иметь вид:
Найдем входящие в коэффициенты регрессии 
и 
с использованием МНК.
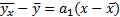
Таким образом, прямая регрессии, построенная в соответствии с МНК, проходит через точку 
, являющуюся центром тяжести поля экспериментальных точек и имеет угловой коэффициент (коэффициент наклона) прямой регрессии относительно оси X равный .
По взаимному расположению прямых регрессии можно судить о тесноте связи между случайными величинами. Отмеченное выше позволяет сформулировать следующие основные свойства выборочного коэффициента корреляции.
1. При 
величины X и Y являются некоррелированными, т.е. они не связаны линейной связью.
2. Если же X и Y распределены нормально, то условие свидетельствует о их полной независимости.
3. Возрастанию абсолютной величины 
соответствует возрастание тесноты линейной корреляционный связи, которая при 
переходит в функциональную.
В практике экспериментальных исследований линейная корреляция встречается достаточно часто. Например, линейной регрессией с коэффициентом корреляции близким к единице описывается взаимосвязь скоростей распространения продольных упругих волн с плотностью, прочностью, динамическим модулем упругости и другими физико-механическими свойствами.
Дата добавления: 2015-02-16; просмотров: 84 | Поможем написать вашу работу | Нарушение авторских прав |