Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Случайное событие. Пространство элементарных событий. Алгебра событий. Несовместимые и совместимые события.

Для математического описания экспериментов со случайными исходами прежде всего потребуется понятие пространства элементарных событий. Пространством элементарных событий будем называть любое множество элементарных событий, обладающих следующими свойствами: во-первых, все они взаимно исключают друг друга, т.е. в результате эксперимента происходит одно и только одно элементарное событие; во-вторых, каждый интересующий нас результат эксперимента может быть описан с помощью элементарных событий, которые будем обозначать

Пространство элементарных событий можно трактовать как множество всех исходов исследуемого случайного явления.

В реальном мире случайное событие - это исход какого-либо эксперимента, который может как произойти, так и не произойти. В том случае, когда число элементарных событий не более чем счетно, случайным событием будем называть любое подмножество элементов из 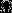(событие А произошло, если произошло какое-либо из элементарных событий 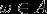). Понятно, что элементарные события являются случайными событиями. В случае, когда пространство 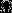несчетно бесконечно, случайными событиями будем называть элементы некоторой – алгебры А подмножеств из .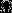

АЛГЕБРА СОБЫТИЙ

Суммой событий А и В называется событие С = А + В, состоящее в наступлении по крайней мере одного из событий А или В.

Пример 1. Испытание: стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадает в мишень первый стрелок, событие В — попадает в мишень второй стрелок. Суммой событий А и В является событие С = А + В — попадает в мишень по крайней мере один стрелок.

Аналогично, суммой конечного числа событий называется событие , состоящее в наступлении хотя бы одного из событий .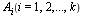

Из определения суммы событий непосредственно следует, что

А + В = В + А.

Справедливо также и сочетательное свойство. Однако

А + А = А (а не 2А, как в алгебре).

Произведением событий А и В называется событие С = А В, состоящее в том, что в результате испытания произошли и событие А, и событие В.

Аналогично, произведением конечного числа событий называется событие 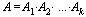, состоящее в том, что в результате испытания произошли все указанные события.

В Примере 1 произведением событий А и В является событие С = А В, состоящее в попадании в мишень двумя стрелками.

Из определения произведения событий непосредственно следует, что

АВ = ВА.

Справедливы также сочетательный и дистрибутивный законы. Однако

АA = А (а не А²).

События А и В, связанные с некоторым опытом, называются совместными, если существует испытание, при котором реализуются оба события.

События А и В, связанные с некоторым опытом, называются несовместными, если не существует испытания, при котором реализуются оба события.

Пример 1. Пусть опыт состоит в бросании игральной кости. Рассмотрим три связанных с этим опытом события:

А - число выпавших очков четное

В - число выпавших очков нечетное

С -число выпавших очков делится на три

Очевидно, что события А и В несовместны, так как не существует испытания, при котором выпавшее число очков будет одновременно и четным, и неетным.

События А и С совместны так как существует испытание (выпадение 6 очков), когда реализуется и А, и С.

События В и С совместны так как существует испытание (выпадение 3очков), когда реализуется и В, и С.