Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Приближенные методы расчета ΔG и константы равновесия

Для расчета термодинамических характеристик химических реакций по способам, изложенным в предыдущем разделе, нужно знать ряд величии, определяемых экспериментально; теплоемкость веществ и ее зависимость от температуры, тепловой эффект и т.п. В некоторых случаях одно или несколько необходимых исходных данных в литературе отсутствует; в этом случае приходится при­бегать к менее точным методам расчета ΔG° и К_Р, не требующим, однако, постановки эксперимента, а основанным лишь на данных о структуре молекул реагирующих веществ и ее изменении в ходе реакции. Для ознакомления с методами расчета можно обратиться, например, к следующим монографиям:

1. Киреев В.А. Методы практических расчетов в термодинамике химических реакций. М., Химия, 1970.

2. Казанская А.С., Скобло В.А. Расчеты химических равновесий. М., Высшая школа, 1974.

В этих и других монографиях разбираются различные методы расчета термодинамических данных и наиболее применимые области их применения.

Равновесие в системах реальных газов

При выводе уравнения изотермы Вант-Гоффа используется уравнение состояния идеальных газов, а все изложенные выше методы расчета термодинамических потенциалов и констант рав­новесия пригодны лишь для газов, близких к идеальным, т. е. на­ходящихся при низких давлениях и достаточно удаленных от со­стояния насыщенного пара. Между тем многие реакции органиче­ского синтеза часто проводятся при высоких давлениях, когда поведение реального газа существенно отклоняется от идеального. Для термодинамического расчета таких систем, чтобы сохранить общий вид термодинамических зависимостей, используют вместо пар­циальных давлений так называемые летучести, или фугитивности газов f, при постоянной температуре удовлетворяющие условию:

(7.11)

При практических расчетах удобнее пользоваться активностью а, которая в общем случае представляет собой отношение летучести вещества в данном состоянии к его летучести f° в стандартном со­стоянии:

(7.12)

Для газов за стандартное принято состояние идеального газа при давлении
1 кгс/см² ≈ 0,1 МПа. Поэтому для идеального газа активность равна его парциальному давлению, а для реаль­ного газа – его летучести. При повышенном давлении они могут существенно различаться, что учитывается коэффициентом актив­ности γ, равным отношению летучести вещества к его парциаль­ному давлению в газовой фазе:

(7.13)

Поскольку при понижении давления все газы стремятся к идеаль­ному состоянию, очевидно, что γ = 1 при Р_общ → 0. Коэффициент активности однозначно связан с так называемым коэффициентом сжимаемости газа z, учитывающим его отклонение от уравнения состояния идеального газа: PV = zRT.

При постоянной темпера­туре имеем:

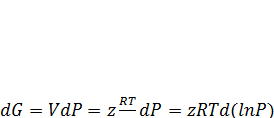
Откуда

d(ln f) = z d(lnP)

d(ln f) – d(lnP) = ( z -1)d(lnP)

d(ln γ) = ( z -1)d(lnP)

Интегрирование последнего уравнения в пределах от 0 до Р дает:

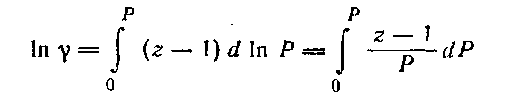
Это уравнение показывает, что коэффициент γ меняется с измене­нием давления и связан с коэффициентом сжимаемости z. Для идеальных газов z = 1 и, следовательно, ln γ = 0, т. е. γ = 1.

Принятое стандартное состояние в газовой фазе позволяет рас­считывать активность как произведение парциального давления на коэффициент активности, поскольку

(7.14)

Уравнение изотермы Вант-Гоффа (7.4) в случае реальных газов преобразуется к виду:

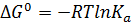(7.15)

с учетом (7.14) можно написать:

(7.16)

Здесь через К_γ обозначена первая дробь, представляющая собой по форме константу равновесия, в которой активности веществ за­менены их коэффициентами активности. Уравнение (11-51) позво­ляет получить окончательное выражение изотермы Вант-Гоффа для реальных систем:

(7.17)

В нем Δ G° соответствует изменению стандартного изобарно-изо­термического потенциала при Р = 1 кгс/см² ≈ 0,1 МПа.

Таким образом, введение понятия активности позволяет свести учет неидеальности газов к вычислению некоторой величины Кγ, завися­щей от стехиометрии реакции и коэффициентов активности реаген­тов. Последние находят из данных по сжимаемости реальных газов и выражают как функции приведенного давления π = Р_общ/Р_кр и приведенной температуры θ = Т/Т_кр, где Р_кр и Т_кр – критические давление и температура данного газа (для водорода, гелия и неона в знаменателе должно стоять ( Р_кр+8) и (Т_кр+8)). Р_общ – общее давление смеси, а не парциальное давление газа, так как его молекулы испытывают влияние и других компонентов смеси. Использование приведенных параметров, вытекающее из принципа соответствен­ных состояний, позволяет применять один и тот же график или одинаковые табличные данные для расчета коэффициентов актив­ности любых газов и паров. Табличные данные и графические зависимости приводятся в справочной литературе.

Экспериментальное определение равновесий

Когда точные данные по термодинамическим функциям или равновесию реакций отсутствуют, для их количественного расчета приходится прибегать к экспериментальному определению равно­весий. Оно позволяет во многих случаях не только измерить кон­станты равновесия, но и сделать полезные, а часто и наиболее точ­ные расчеты других термодинамических функций – изменения изобарно-изотермических потенциалов, тепловых эффектов и т. д.

Методы экспериментального определения констант равновесия основаны на анализе состава реакционной смеси после достиже­ния ею состояния химического равновесия. Для получения надеж­ных результатов, кроме обычной проверки на воспроизводимость, необходимо ставить эксперименты таким образом, чтобы состояние равновесия достигалось с разных сторон, т. е. при первоначальном протекании как прямой, так и обратной реакции (в разных опы­тах). Только совпадение (в пределах ошибки опыта) аналитиче­ских данных по составу реакционной массы может в этом случае гарантировать, что изучается истинное равновесие.

Основные экс­периментальные приемы для измерения констант равновесия де­лятся на две группы: 1) статические методы; 2) динамические ме­тоды.

При статических методах используют периодический реактор и ведут процесс до тех пор, пока результаты анализа реакционной массы не окажутся практически совпадающими. Начиная с этого момента, кинетические кривые для всех продуктов будут парал­лельны оси абсцисс, что и отвечает состоянию равновесия, исходя из которого, при известной стехиометрии, можно вычислить кон­станту равновесия.

Динамические методы основаны на использовании непрерывных реакторов вытеснения и особенно удобны для изучения равновесия гетерогенных каталитических реакций. В этом случае постепенно уве­личивают время пребывания реакционной смеси в аппарате, пока на выходе не будет достигнут практически постоянный состав, со­ответствующий равновесию. Основные трудности здесь такие:

- необходимость поддержания в реакторе строго заданной темпера­туры, не меняющейся по длине (хотя бы на достаточно длинном участке перед выходом из реактора);

- необходимость резкого тор­можения реакции на выходе из аппарата – путем охлаждения или химического разложения, чтобы воспрепятствовать смещению рав­новесия при последующем хранении и анализе проб, так называемая – закалка.

Естественно, при динамических методах для более точного опре­деления необходим ряд параллельных опытов с подсчетом средней константы равновесия и доверительного интервала ее величины.

Равновесие жидкофазных реакций

Расчет констант равновесия и составов равновесных смесей для гомогенных жидкофазных реакций или для взаимодействия газов с жидкостями представляет большой практический интерес, по­скольку такие процессы часто встречаются в техно­логии органических соединений. Эти расчеты имеют ряд особенностей по сравнению с рас­четами газофазных реакций, что обусловлено спецификой жидкого состояния веществ и растворов.

Приведенный нами ранее вид уравнения изотермы Вант-Гоффа (7.4) относится к газовой смеси. Однако можно показать, что такое же уравнение справедливо для любого состояния веществ:

(7.18)

Из уравнения (7.18) следует, что константа равновесия жидкофазной реакции, выраженная через активности, может быть рас­считана обычным путем – по изменению стандартного изобарно-изотермического потенциала. Для этого надо установить стандарт­ное состояние для жидкостей и растворов и принять способ расчета или экспериментального определения активностей.

Для жидкостей стандартным принято их состояние в виде чи­стой жидкости при соответствующей температуре. Стандартные термодинамические параметры ряда жидкостей при 25 °С приве­дены в справочниках. Для пересчета на другие температуры можно воспользоваться методом Темкина – Шварцмана, считая, что тепло­емкость постоянна (поскольку изменение температур для жидко­фазных реакций невелико). Другой способ состоит в использований табличных или расчетных данных по стандартным изобарно-изотермическим потенциалам образования веществ для газообраз­ного состояния Δ Gº_f,Г. Поскольку они относятся к давлению газа (пара) 1 кгс/см² (≈ 0,1 МПа), при их пересчете следует учесть Δ Gº пара при изменении давления от 1 кгс/см² до давления, соответствующего равновесному давлению пара Р₀ над жидкостью при данной температуре. Последующий перевод вещества из состояния пара в находящуюся с ним в равновесии жидкость не ведет к из­менению Δ Gº. Таким образом, получаем:

(7.19)

Эти данные оказываются вполне достаточными при термодинами­ческом расчете равновесий для идеальных систем, подчиняющихся законам Рауля и Генри. Поскольку активность равна отношению летучестей в данном и стандартном состоянии (a = f / f ^o), а лету­честь вещества в растворе всегда равна летучести пара, находя­щегося с ним в равновесии (которую можно считать равной его парциальному давлению P_i), по закону Рауля имеем:

f_ж = P_i = P_i,0N_i

где N_i – мольная доля вещества в растворе. Отсюда получаем:

Таким образом, для идеальных растворов, когда стандартным при­нято состояние чистой жидкости, активность вещества равна его мольной доле, а константу равновесия следует выражать не через концентрации (как это часто принято), а через мольные доли:

(7.20)

В свою очередь, K_N связана с Δ Gº известным соотношением:

(7.21)

Основанные на изложенном методе расчеты равновесий жидкофазных реакций, дают вполне удовлетворительные результаты для смесей и растворов углеводородов и галогенпроизводных. В мень­шей степени они справедливы для простых эфиров, сульфидов, меркаптанов, кетонов, альдегидов, аминов и нитросоединений – в реакциях их изомеризации, гидрирования, алкилирования и др., в которых другими реагентами или продуктами не являются ве­щества, способные нарушить идеальность системы.

Интересно выявить соотношения между константами равнове­сия в газовой и жидкой фазах для идеальных систем. Согласно предыдущему, имеем:

Откуда

(7.21)

Следовательно, более простой путь для расчета равновесия в иде­альных растворах состоит в определении изложенными ранее спо­собами константы равновесия в газовой фазе (К_P) и умножении ее на обратную величину отношения произведений равновесных давлений паров над чистыми жидкими продуктами и исходными реагентами, причем давления взяты в степенях, равных стехиометрическим коэффициентам. Так, например, для изомеризации н-бутана в изобутан стандартное изменение изобарно-изотермического потен­циала равно Δ Gº₂₉₈ = -900 кал/моль (-3767 Дж/моль), что дает константу равновесия для газовой фазы:

lgK _P,298 = 900/(2,303·298·1,987) = 0,657

K _P,298 = 4,56

Отсюда константа равновесия той же реакции в жидкой фазе равна:

4,56 = 3,2

где 3,43 и 2,40 кгс/см² – давления насыщенных паров изобутана и н-бутана при 25°С. Полученная величина К_Р близка к найденной экспериментально.

Для неидеальных растворов расчет равновесий существенно осложняется. Здесь стандартным остается для растворителя со­стояние чистой жидкости, а для растворенного вещества – гипоте­тическое состояние в растворе с активностью, равной единице, но с такими же термодинамическими и другими параметрами, кото­рыми вещество обладает в бесконечно разбавленном растворе.

В реальных растворах активность растворенного вещества равна его мольной доле только при бесконечном разбавлении. По­этому определение стандартных термодинамических параметров возможно, например, по экспериментальным данным о зависимости давления паров растворенного вещества над раствором при посте­пенном разбавлении. Эта зависимость подчиняется обобщенному уравнению

(7.22)

где активность пара принята равной его парциальному давле­нию P_i,0. При бесконечном разбавлении записанная зависимость превращается в другую:

(7.23)

Откладывая на графике против (рис. 7.1) и экстраполи­руя кривую к , получают величину константы распределе­ния К_i. После этого находят давление паров вещества над гипоте­тическим стандартным раствором с
а_i = 1, т.е. ­ .

Изменение стандартного изобарно-изотермического потенциала образования растворенного вещества можно затем вычислить из ΔG⁰ _{f ,г} с поправкой на изменение давления пара от ­ до 1 кгс/см²:

(7.24)

Например, для раствора ацетона в сероуглероде при 37 °С по зависимости давления паров ацетона от разбавления найдена K_i = 0,304 см²/кгс. Тогда давление его пара над стандартным раствором будет равно 1: 0,304 = 3,29 кгс/см² и стандартный изобарно-изотермический потенциал раствора ацетона в сероуглероде составит:

= -36 500 + RT ln 3,29 = -35 770 кал/моль =

= -149 733 Дж/моль

Алгебраически складывая найденные значения ΔG⁰ _{f ,ж} для всех компонентов, получаем изменение стандартного изобарно-изотер­мического потенциала реакции, известным образом связанное с К_а:

При таком расчете можно исключить из рассмотрения твердые компоненты, так как их активность всегда равна единице и Δ G⁰_f = -RTlna = 0, а для реагента-растворителя нужно лишь ввести поправку, учитывающую, что его активность равна отноше­нию давления паров над данным раствором и над чистой жидкостью:

Для равновесий в системе газ – жидкость не требуется рассчи­тывать Δ G⁰_f для растворенного газа, так как в этом случае поль­зуются другим выражением константы равновесия, включающим парциальные давления газообразных веществ.

Для неидеальных растворов, когда на термодинамические па­раметры компонентов влияет их взаимодействие не только с рас­творителем, но и друг с другом (образование комплексов, особен­но за счет специфической сольватации между компонентами реак­ции), изложенные методы термодинамического расчета равнове­сий становятся непригодными. В этом случае требуется знать экспериментальные данные по изменению давления паров каждого вещества над многокомпонентными растворами при их постепен­ном разбавлении, что увеличивает объем необходимого исследова­ния и усложняет расчеты.

В связи с изложенными трудностями термодинамического рас­чета жидкофазных реакций, для них бóльшее значение, чем для газофазных процессов, имеет экспериментальное определение рав­новесных составов смеси и констант равновесия. При этом непо­средственно находят равновесные концентрации веществ, из кото­рых легко рассчитать мольные доли и далее К_С и K_N. Эти результаты достаточны для определения состава равновесных смесей при любом соотношении исходных реагентов в случае идеальных си­стем. Однако принимать К_С и K_N постоянными для реальных рас­творов было бы ошибочным. Так, при кислотно-каталитической этерификации спиртов карбоновыми кислотами К_С и K_N суще­ственно увеличиваются при повышении концентрации катализа­тора, что зависит от преимущественной сольватации протона бо­лее основной водой; это ведет к снижению действующей концентрации (активности) воды и смещению равновесия вправо. Точно так же при изомеризации ди- или полиалкилбензолов в присут­ствии хлористого алюминия с ростом концентрации AlCl₃ увели­чивается равновесное содержание 1,3- или 1,3,5-изомеров, обра­зующих с катализатором более стабильные комплексы.

Эти примеры показывают, что для неидеальных систем экспе­риментально найденные мольные доли веществ при равновесии надо выразить через активности, чтобы определить величину дей­ствительно постоянной константы Кa.

При жидкофазных реакциях объем обычно меняется мало, и поэтому использованные ранее приемы расчета равновесных сме­сей в этом случае применимы для любых реакций, в том числе для идущих с изменением общего числа молей веществ. Как и раньше, равновесные концентрации выражают как функцию одной пере­менной – равновесной степени конверсии или равновесной концен­трации ключевого вещества, которые находят затем из выражения для константы равновесия.

Вопросы и упражнения для самостоятельного решения

1. Какая разница между изменениями изобарно-изотермического потенциала ΔG и стандартного изобарно-изотермического потенциала ΔG°? Какой из них при равновесии равен нулю?

2. Чему равно изменение энтропии и изобарно-изотермического потенциала при равновесном превращении вещества из жидкости в пар при постоянных тем­пературе и давлении? То же самое для химической реакции?

3. Объясните физический смысл, размерность и взаимные связи между лету­честью, активностью, парциальным давлением и коэффициентом активности для реальных газов.

4. Каково соотношение между термодинамическими функциями одного и того же вещества, находящегося в стандартном состоянии в газе и растворе?

5. Для реакции А + Y = В имеем К_P = 1,0. Какими двумя способами мо­жно добиться, чтобы равновесная степень превращения вещества А достигла 90%?

6. Для последовательной реакции

выведите аналитиче­ское решение для содержания (мольной доли) каждого вещества в равновесной смеси в зависимости от констант К₁ и К₂.