Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Означення та умови існування визначеного інтеграла.

Оскільки ми побачили, що дві різні задачі приводять до однієї математичної моделі, ми тепер не будемо прив’язуватись до конкретної задачі з навколишньої дійсності, а розглянемо проблему в абстрактному сенсі. Отже нехай ми маємо деяку функцію , яка визначена на відрізку . Розіб’ємо цей відрізок на частин довільно обраними точками ділення:

.

На кожному з частинних відрізків довільним чином оберемо точку і побудуємо суму:

, (8.2.1) де – довжина відрізка . Сума (8.2.1) називається інтегральною сумою функції , яка відповідає даному розбиттю відрізка на частинні та даному вибору проміжних точок .

Легко помітити, що з геометричної точки зору інтегральна сума у випадку, коли , дорівнює площі ступінчатої фігури (рис. 8.3).

Позначимо і назвемо цю величину рангом розбиття. Це буде означати, що жоден з частинних відрізків за довжиною не перевищує величини .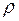

Означення. Якщо існує скінченна границя інтегральної суми (8.2.1) при , яка не залежить від засобу розбиття відрізка на частинні і не залежить від засобу обрання проміжних точок , то ця границя називається визначеним інтегралом функції на відрізку і позначається символом:

.

Тобто:

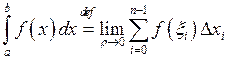. (8.2.2)

Символ був введений Г.Лейбніцем у 1686 році. Цей символ є дещо деформованою буквою (перша буква слова Summa). Термін «інтеграл» (від латинського integer – цілий) був запропонований у 1696 році Іоганом Бернулі. Наведене означення інтеграла належить Бернгарду Ріману (1826–1866), він же сформулював умови його існування. Тому таким чином введений інтеграл називається інтегралом Рімана.

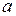Якщо границя (8.2.2) існує, то функція називається інтегровною на відрізку . Числа і називаються відповідно нижньою та верхнею межею інтегрування. Функція називається підінтегральною функцією, а вираз 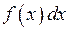називається підінтегральним виразом. Змінна називається змінною інтегрування, а проміжок – проміжком інтегрування.

Повертаючись до розглянутих у пункті 8.1 задач, тепер можна сказати, що

1) площа криволінійної трапеції, обмеженої прямими і графіком функції , дорівнює визначеному інтегралу від цієї функції на відрізку :

.

У цьому полягає геометричний зміст інтеграла.

2) робота змінної сили , що діє вздовж відрізка , дорівнює визначеному інтегралу від сили:

.

У цьому полягає фізичний зміст інтеграла.

Виникає питання, яким умовам повинна задовольняти інтегровна на відрізку функція ? Відповідь на це питання дають наступні теореми, яки ми наводимо без доведення*.

Теорема 1 (необхідна умова інтегровності). Якщо функція інтегровна на відрізку , то вона обмежена на цьому відрізку.

Теорема 2 (достатня умова інтегровності). Якщо функція неперервна на відрізку , то вона інтегровна на цьому відрізку.

Можна показати, що теорема 1 дає саме необхідну умову інтегровності, але не достатню (з обмеженості функції на відрізку не випливає її інтегровність на цьому відрізку – існують обмежені неінтегровні функції). В той же час теорема 2 дає саме достатню умову інтегровності, але не необхідну (інтегровними можуть будуть і деякі розривні функції).

Наведемо приклад обчислення визначеного інтеграла, як кажуть, за означенням.

Приклад. Обчислити:

.

Розіб’ємо відрізок довільним чином на частинні відрізки і складемо інтегральну суму:

.

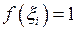Незалежно від обрання точок буде виконано: , тому:

.

І отже:

.

Для довільних функцій обчислення інтеграла за означенням досить складне, тому пізніше ми познайомимось з іншим методом його обчислення, правда який «працює» лише для неперервних функцій.