Читайте также:
|
Перейдем к решению примеров, в которых требуется вычислить приближенное значение определенного интеграла методом прямоугольников.
В основном, встречаются два типа задач. В первом случае задается количество интервалов, на которые разбивается отрезок интегрирования. Во втором случае задается допустимая абсолютная погрешность.
Формулировки задач примерно следующие:
· вычислить приближенно определенный интеграл методом прямоугольников, разбив отрезок интегрирования на n частей;
· Методом прямоугольников найти приближенное значение определенного интеграла с точностью до одной сотой (одной тысячной и т.п.).
Разберем каждый случай.
Сразу оговоримся, что в примерах подынтегральные функции будем брать такие, чтобы можно было найти их первообразные. В этом случае мы сможем вычислить точное значение определенного интеграла и сравнить его с приближенным значением, полученным по методу прямоугольников.
Пример.
Вычислить определенный интеграл 
методом прямоугольников, разбив отрезок интегрирования на 10 частей.
Решение.
В нашем примере a = 4, b = 9, n = 10, 
.
Внимательно посмотрим на формулу прямоугольников 
.
Чтобы ее применить, нам нужно вычислить шаг h и значения функции в точках 
.
Вычислим шаг: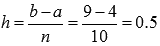 
.
Так как 
, то 
.
Для i = 1 имеем 
. Находим соответствующее значение функции 
.
Для i = 2 имеем 
. Находим соответствующее значение функции 
.
И так продолжаем вычисления до i = 10.
Для удобства представим результаты в виде таблицы.
Подставляем полученные значения в формулу прямоугольников:
Значение исходного определенного интеграла можно вычислить по формуле Ньютона-Лейбница:
.
Первообразная 
подынтегральной функции была найдена интегрированием по частям.
Как видите, точное значение определенного интеграла отличается от значения, полученного по методу прямоугольников для n = 10, менее чем на шесть сотых долей единицы.
Графическая иллюстрация.
Пример.
Вычислите приближенное значение определенного интеграла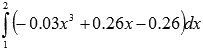 
методами левых и правых прямоугольников с точностью до одной сотой.
Решение.
По условию имеем a = 1, b = 2,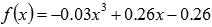 
.
Чтобы применить формулы правых и левых прямоугольников нам необходимо знать шаг h, а чтобы вычислить шаг h необходимо знать на какое число отрезков n разбивать отрезок интегрирования. Так как в условии задачи нам указана точность вычисления 0.01, то число n мы можем найти из оценки абсолютной погрешности методов левых и правых прямоугольников.
Нам известно, что 
. Следовательно, если найти n, для которого будет выполняться неравенство 
, то будет достигнута требуемая степень точности.
Найдем 
- наибольшее значение модуля первой производной подынтегральной функции 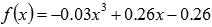на отрезке [1; 2]. В нашем примере это сделать достаточно просто.
Графиком функции производной подынтегральной функции является парабола, ветви которой направлены вниз, на отрезке [1; 2] ее график монотонно убывает. Поэтому достаточно вычислить модули значения производной на концах отрезка и выбрать наибольшее:
В примерах со сложными подынтегральными функциями Вам может потребоваться теория раздела наибольшее и наименьшее значение функции.
Таким образом:
Число n не может быть дробным (так как n – натуральное число – количество отрезков разбиения интервала интегрирования). Поэтому, для достижения точности 0.01 по методу правых или левых прямоугольников, мы можем брать любое n = 9, 10, 11, … Для удобства расчетов возьмем n = 10.
Формула левых прямоугольников имеет вид 
, а правых прямоугольников 
. Для их применения нам требуется найти h и 
для n = 10.
Итак, 
Точки разбиения отрезка [a; b] определяются как 
.
Для i = 0 имеем 
и 
.
Для i = 1 имеем 
и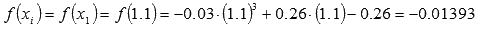 
.
И так далее до i = 10.
Полученные результаты удобно представлять в виде таблицы:
Подставляем в формулу левых прямоугольников:
Подставляем в формулу правых прямоугольников:
Вычислим точное значение определенного интеграла по формуле Ньютона-Лейбница:
Очевидно, точность в одну сотую соблюдена.
Графическая иллюстрация.
Дата добавления: 2015-09-11; просмотров: 106 | Поможем написать вашу работу | Нарушение авторских прав |
| <== предыдущая лекция | | | следующая лекция ==> |
| Оценка абсолютной погрешности метода средних прямоугольников. | | | Замечание. |