Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Абсолютная сходимость несобственных интегралов.

До сих пор при анализе сходимости несобственных интегралов мы предполагали, что подинтегральная функция принимает только положительные значения. Откажемся от этого предположения. Будем исследовать сходимость несобственных интегралов первого рода вида 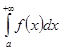, где 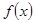может принимать значения любого знака. Полученные результаты переносятся по аналогии на остальные несобственные интегралы первого и второго рода.

Интеграл 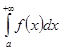называется абсолютно сходящимся, если сходится несобственный интеграл .

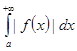Теорема. Если интеграл 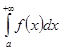абсолютно сходится, то он сходится.

Доказательство. Введем в рассмотрение две вспомогательные функции . Эти функции принимают только положительные значения. Кроме того, . По первому признаку сравнения из абсолютной сходимости интеграла 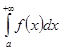, т.е. из сходимости интеграла 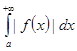следует сходимость интегралов 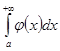, . Тогда сходится интеграл . Теорема доказана.

Пример. абсолютно сходится, так как а интеграл сходится.