Читайте также:
|
Сформулируем теорему, которая позволяет определять промежутки выпуклости функции.
Теорема.
Если функция y=f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство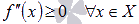 
(
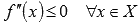), то график функции имеет выпуклость направленную вниз (вверх) на Х.
Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить неравенства 
и 
соответственно.
Следует отметить, что точки, в которых функция y=f(x) определена, а вторая производная не существует, будем включать в интервалы вогнутости и выпуклости.
Разберемся с этим на примере.
Пример.
Выяснить промежутки, на которых график функции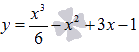 
имеет выпуклость направленную вверх и выпуклость направленную вниз.
Решение.
Областью определения этой функции является все множество действительных чисел.
Найдем вторую производную.
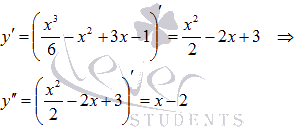
Область определения второй производной совпадает с областью определения исходной функции, поэтому, чтобы выяснить интервалы вогнутости и выпуклости, достаточно решить и соответственно.
Следовательно, функция выпуклая вниз на интервале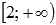 
и выпуклая вверх на интервале 
.
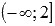Дата добавления: 2015-09-10; просмотров: 88 | Поможем написать вашу работу | Нарушение авторских прав |