Читайте также:
|
Свойства неопределенного интеграла можно условно разделить на две группы. В первую группу собраны свойства, вытекающие из того, что интегрирование – операция, обратная дифференцированию. Во вторую группу собраны свойства линейности. Эти свойства вытекают из того, что интегрирование, как и дифференцирование – линейная операция и определяют линейную операцию.
Первая группа свойств.
1) 
.
2) 
3) 
4) 
.
Докажем первое свойство.
Так как 
Здесь 
- первообразная для 
.
Докажем второе свойство.
Обозначим 
Тогда 
, а 
по первому свойству. Поэтому функции 
являются первообразными для функции 
. Следовательно, по теоремам о первообразных, они различаются на константу, т.е. 
или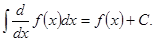 
Третье свойство следует из первого: 
Четвертое свойство следует из второго, если вспомнить, что с дифференциалом первого порядка можно обращаться как с алгебраическим выражением (свойство инвариантности формы записи первого дифференциала).
Поэтому надо доказать два первых свойства.
Вторая группа свойств.
1) свойство суперпозиции 
2) свойство однородности 
.
Доказательства того и другого свойств проводятся аналогично. Дифференцируем (по свойствам первой группы) левую и правую часть равенства, приходим к тождеству. Затем из теорем о первообразных заключаем, что левая и правая часть равенства, как первообразные одной и той же функции, различаются на константу. Эта константа может быть формально включена в неопределенный интеграл в левой или правой части равенства.
Для того, чтобы вычислить интеграл от функции, проще всего «угадать» первообразную для этой функции по таблице для производных, переписав эту таблицу в обратном порядке. Запишем интегралы для основных элементарных функций.
1) 
. Эти формулы лучше запомнить, они очень часто встречаются.
2) 
3) 
4) 
Справедливость этих формул легко проверить, дифференцируя правую часть соотношения и получая подинтегральную функцию.
Лекция 2. Методы интегрирования и таблица интегралов.
Метод подведения под дифференциал.
Пусть известен интеграл 
( - первообразная для функции ). Тогда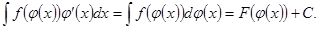 
Главное здесь – «догадаться», как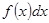 
представить в виде 
. 
Доказательство. 
по теореме о сложной функции. Следовательно, функция 
и 
являются первообразными для функции 
и, по теоремам о первообразных, различаются на константу.
Этот метод применяется часто. Например, 
, 
.
Метод замены переменной.
Это – универсальный метод, метод подведения под дифференциал является частным случаем метода замены переменной.
Теорема. Пусть функция 
непрерывно дифференцируема в некоторой области и имеет непрерывно дифференцируемую обратную функцию 
. Тогда 
где .
Доказательство. Дифференцируя обе части, используя теоремы о производной сложной функции и инвариантность формы записи первого дифференциала, получим тождество дифференциалов.
, где . Из него следует равенство интегралов в левой и правой частях.
Заметим, что требования к обратной функции нужны, чтобы суметь возвратиться обратно, от переменной 
к переменной 
.
Для вычисления интегралов вида 
, если вместо него удобно вычислять интеграл 
, пользуются методом интегрирования по частям.
= 
- ,
если интегралы в обеих частях соотношения существуют.
Докажем справедливость этой формулы. Дифференцируя произведение функций, получим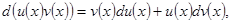 
или
.
Интегралы левой и правой частей существуют(
).
Интегрируя, получим нужное соотношение.
Примеры.
.
Вычислим интегралы 
, 
.
, 
.
Теперь, подставляя второй интеграл в первый, получим
.
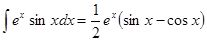Аналогично, подставляя первый интеграл во второй, получим
.
Пополним таблицу интегралов, применяя методы интегрирования (в первой лекции получены четыре интеграла).
5. 
6. 
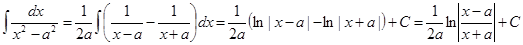
7. 
8. 
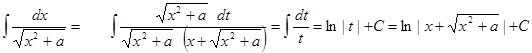
Здесь сделана замена переменной, подстановка 
- одна из подстановок Эйлера,
, 
, 
.
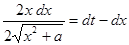9. 
(
)
.
.
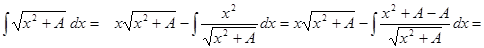
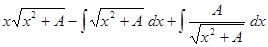Перенося искомый интеграл из правой части в левую часть, получим
10. 
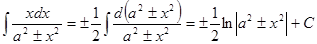
11. 
12. 
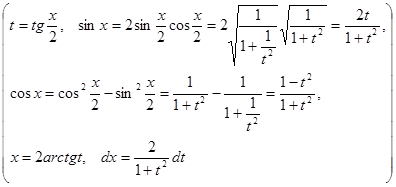
13. 
- вывести самостоятельно.
Эти соотношения представляют собой таблицу основных интегралов.
Дата добавления: 2015-09-10; просмотров: 31 | Поможем написать вашу работу | Нарушение авторских прав |