Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Дифференциальное уравнение теплопроводности. Краевые условия.

Условности:

1. Теплофизические свойства системы: , , .

2. Микрочастицы тела неподвижны.

3. Внутренние источники теплоты распределены в теле равномерно.

, где – коэффициент температуропроводности, характеризующий скорость изменения температуры в любой точке тела, ;

– теплоемкость тела; – плотность тела; – объемная плотность тепловыделения, вm/м³; 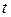– температура; 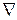– оператор Лапласа.

Краевые условия

Дифференциальное уравнение описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые ха­рактеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает процесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды tж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

,

где tc — температура поверхности тела; a — коэффициент пропорцио­нальности, называемый коэффициентом теплоотдачи, Вт/(м2×К).

,получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.