Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Дифференциальное уравнение вынужденных электромагнитных колебаний. Резонанс напряжения и резонанс тока

Подключим колебательный контур, сопротивление которого равно R, к генератору переменной электродвижущей силы

e = e_т cos Ω t,

где e_т и Ω - амплитуда и частота напря­жения (ЭДС), вырабатываемого генератором (рис.9.7). В этом случае правило Кирхгофа дает уравнение

Рис. 9.7. Колебательный контур с генератором ЭДС

Q/C + RI = -LdI/dt + e_т cos Ω t,

которое преобразуем при помощи фор­мул (9.6) и (9.7) к виду

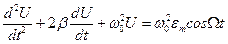(9.52)

где функция U = U(t) описывает колебания напряжения на конденса­торе. Общее решение этого уравнения представляет собой сумму двух функций:

U(t) = U_cв(t) + U_в(t), (9.53)

где функция U_cв(t) является общим решением (9.25) уравнения (9.23). Эта функция описывает так называемые свободные колебания. Функция

U_в(t) есть частное решение уравнения (9.52). Она описывает вынужден­ный колебания, обусловленные действием подключенного к контуру гене­ратора. Свободные колебания затухают с течением времени. Вынужден­ные колебания совершаются до тех пор, пока не перестанет действовать генератор. После того как прекратятся свободные затухающие колеба­ния (т.е. обратится в ноль первое слагаемое в формуле (9.53), описываю­щее эти колебания), в контуре будут происходить только вынужденные колебания, которые в таком случае называются установившимися.

Будем искать частное решение уравнения (9.52), которое описывает установившиеся колебания, в виде

U = U_в(t) = U_m cos(Ωt + y),

где U_m - амплитуда вынужденных колебаний напряжения на конденса­торе, y - начальная фаза этих колебаний. Найдем функции

dU/dt = - Ω U_m sin (Ωt + y), d²U/dt² = - Ω² U_m cos (Ωt + y),

Подстановка функции (9.54) и ее производных в уравнение (9.52) приво­дит к равенству

U_m ((w₀² -Ω²) cos (Ωt + y)-2 β Ωsin(Ωt + y)) = w₀² e_т cos Ωt.

Преобразуем это равенство при помощи тригонометрических формул

cos (Ωt + y) =cos Ωt cos y - sinΩtsin y,

sin (Ωt + y) = sin Ωt cos y + cos Ωtsin y,

Сгруппировав слагаемые, содержащие cos Ωt иsinΩt, получим равен­ство

U_m ((w₀² -Ω²) cos y -2 β Ωsin y)cos Ωt +

+U_m (-(w₀² -Ω²)sin y -2 β Ω cosy)sin Ωt = w₀² e_т cos Ωt.

Это равенство будет выполняться при любых значениях времени t, если равны коэффициенты при cos Ωt иsinΩt в левой и правой частях равен­ства:

U_m ((w₀² -Ω²) cos y -2 β Ωsin y) = w₀² e_т

(9.55)

U_m (-(w₀² -Ω²)sin y -2 β Ω cosy) = 0 (9.56)

Возведем уравнения (9.55) и (9.56) в квадрат и сложим полученные таким
образом уравнения. Придем к уравнению

U_m² ((w₀² -Ω²)² +4 β² Ω²) = w₀⁴ e_т²

из которого найдем, что амплитуда вынужденных колебаний напряже­ния на конденсаторе

U_m = U_m (Ω) = w₀² e_т /√((w₀² -Ω²)² +4 β² Ω²)

Изуравнения (9.56) найдем начальную фазу y вынужденных колебаний

tg y = - 2 β Ω /(w₀² -Ω²) (9.58)

Как видно из формулы (9.57), амплитуда вынужденных колебаний на­пряжения на конденсаторе зависит от частоты генератора электродвижу­щей силы. При Ω = 0 генератор вырабатывает постоянное напряжение e_т. В этом случае ток в контуре отсутствует и напряжение на конденса­торе равно напряжению на клеммах генератора U_m = e_т. При увеличе­нии частоты генератора амплитуда U_m вынужденных колебаний напря­жения на конденсаторе увеличивается, достигая наибольшего значения, когда частота генератора принимает значение Ω_р, называемое резонанс­ной частотой; а затем при дальнейшем увеличении Ω уменьшается до нуля. График зависимости U_m = f_m(Ω), определяемой формулой (9.57), представлен на рис. 9.8. Такого вида кривые называются резонансными, а само явление увеличения амплитуды вынужденных колебаний, когда их частота приближается к резонансному значению, - резонансом

U_m

0 Ω_р Ω

Рис. 9.8. Резонанс напряжения на конденсаторе

Резонансную частоту Ω_р можно най­ти из условия максимума функции U_m = U_m (Ω)

dU_m/dΩ=0

Подставив в это условие производную функции (9.57), получим уравнение

-w₀² +Ω² +2 β² =0 (9.59)

из которого найдем, что

Ω_р = √(w₀² - 2 β²)

Этому значению частоты соответствует наибольшее (резонансное) значе­ние амплитуды напряжения

U_mp = w₀² e_т /(2 β √(w₀² - β²))

Анализируя формулу (9.59), приходим к выводу, что функция U_m = U_m (Ω) имеет максимум при условии, что

β <w₀/√2

т.е. когда коэффициент затухания β принимает достаточно низкие зна­чения. Если свободные колебания в контуре затухают очень быстро (β >w₀/√2 ), то резонанс невозможен. Чем меньше коэффициент за­тухания β, тем ближе значение Ω _р резонансной частоты к собственной частоте w₀ контура и тем больше резонансное значение U_mp амплитуды напряжения, как это видно из формулы (9.60).

Подставив функцию (9.54) в формулу (9.8), найдем зависимость силы тока от времени

I = I_в(t) = -C Ω U_m sin (Ωt + y) = I_m cos (Ωt + y +p/2),(9.61)

которое описывает установившиеся вынужденные колебания силы тока в контуре. Амплитуда этих колебаний, как следует из формул (9.57) и (9.61), будет

I_m = I_m (Ω) = C Ω U_m = C Ωw₀² e_т /(√((w₀² -Ω ²)² + 4 β ² Ω ²), (9.62)

Нетрудно видеть, что это выражение при любых значениях частоты Ω неотрицательно. При Ω = 0 и Ω →∞ амплитуда силы тока обращается в ноль. Найдем наибольшее значение амплитуды I_т силы тока из условия

dI_т/dΩ= 0.

Подставив функцию (9.62) в это условие, после ее дифференцирования и элементарных преобразований полученного уравнения найдем, что ам­плитуда I_т силы тока достигает наибольшего значения при

Ω = w₀

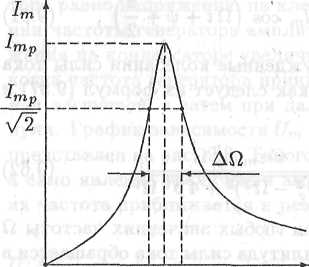
т.е. резонансная частота для силы тока равна собственной частоте кон­тура. График функции 1_т = I_m (Ω) представлен на рис. 9.9.

Резонансное значение силы тока

I_mp = I_m (w₀) = C w₀² e_т /(2 β) = e_т /R, (9.63)

Интересно отметить, что это значение совпадает со значением силы по­стоянного тока, который протекает по проводнику сопротивления R, ко­гда к нему приложено постоянное напряжение e_т.

Найдем значения частоты Ω, которым соответствует значение ампли­туды силы тока в \/2 раз меньшее резонансного значения:

I_m (Ω) = I_mp/ √2 (9.64)

При помощи формул (9.62) и (9.63) это уравнение можно записать так:

2√2 β Ω = √((w₀² -Ω ²)² + 4 β ² Ω ²)

После возведения этого уравнения в квадрат и простых преобразований придем к уравнению

(Ω +w₀)| Ω -w₀| = 2 β Ω.

Из этого уравнения найдем, что ши­рина ΔΩ (рис. 9.9) резонансной кри­вой на уровне I_mp/√2

ΔΩ =2 | Ω -w₀| = 4 β Ω/(Ω +w₀)

Так как для частот

ΔΩ = (w₀- ΔΩ /2, w₀+Ω/2)

справедливо приближенное равенство

ΔΩ ≈ w₀

будем иметь

ΔΩ ≈ 2β. (9,65)

0 w₀ Ω

Рис. 9.9. Резонанс силы тока в колебательном контуре

При помощи соотношения (9.31), которое справедливо при β<<w ₀,этой формуле можно придать вид

ΔΩ/w₀ =1/Q

Таким образом, приходим к заключению, что относительная ширина ΔΩ/w₀ резонансной кривой обратно пропорциональна добротности конТура Q. Отсюда следует, что чем выше добротность контура, тем "острее" резонансная кривая.