Читайте также:
|
Формула Пуассона
Рассмотри волновое уравнение
(1)
и будем искать его решение, удовлетворяющее начальным условиям
(2)
Будем предполагать, что 
Лемма. Функция, заданная интегралом
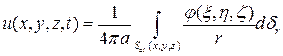(3)
с произвольной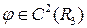 
является решение (1).
Здесь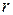 
= 
Доказательство. Пусть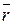 
вектор из центра (
) в точку 
на поверхности сферы. Направляющий вектор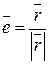 
имеет координаты 
, где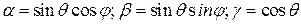 
- сферические координаты с центром в точке (), 
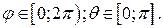
Координаты точки сферы 
можем записать в виде
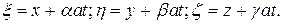
Когда точка описывает , точка 
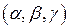описывает сферу 
. Между соответствующими элементами площаде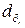й 
и 
имеется соотношение 
Интеграл (3) может быть представлен в виде
(4)
Отсюда,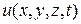 
имеет нулевые производные до 2 порядка, (т.к. 
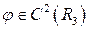). Из (4) имеем
Вернемся к первоначальной области интегрирования
.
Продифференцируем теперь (4) по 
Заметим, что – направляющий вектор радиуса сферы =>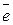 
– направляющий вектор внешней нормали. Применим формулу Остроградского
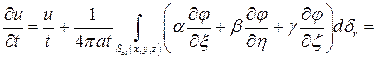
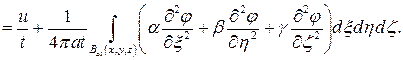
Положим
.
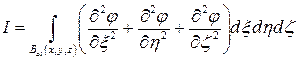Имеем
.
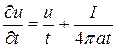Дифференцируем по времени
Замечание: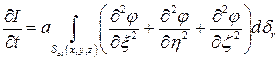 
Действительно, в сферических координатах
Дифференцируя по , получим
Замечание доказано.
Сравнивая (5),(7),(8) видим
Лемма доказана.
Из формулы (4) следует, что
.
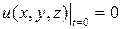Из формулы (6) следует
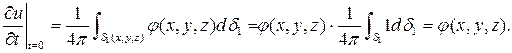
Итак,
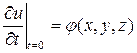(9)
Если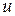 
– решение (1) с начальными данными (9), то легко видеть, что функция 
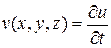так же есть решение (1), причем
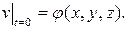
Но, так как
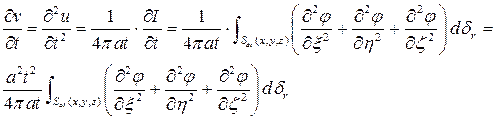
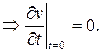
Итак:
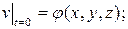
(10)
Возьмем теперь вместо функции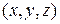 
в (9) функцию 
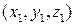, а в (10) - функцию 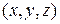и, сложив построенные по нашим функциям решения, будем иметь решение уравнения (1) удовлетворяющее условиям (2).
Таким образом, решение волнового уравнения (1), удовлетворяющее начальным условиям (2), запишется в виде
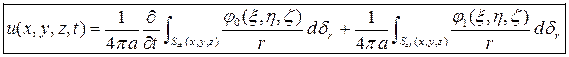
Эта формула называется формулой Пуассона.
Непрерывная зависимость решения от начальных данных.
Все формулы, дающие решение задачи Коши для волнового уравнения, содержат интегралы от начальных функций, умноженных на определенные функции и производные по времени от таких интегралов. Возьмем формулу Пуассона. Пусть по зафиксированному нами 
выполняются следующие условия: (нормы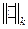 
в шкале 
).
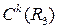Оценим интегралы
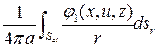
и
.
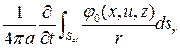Тогда
.
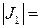
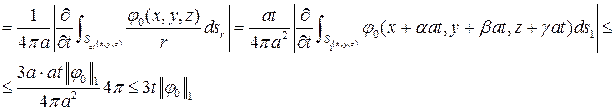
Если условиям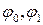 
соответствует решение 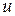, а условиям 
- решение 
, то
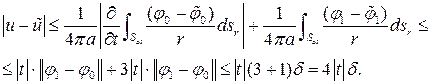
Пусть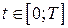 
. По произвольному 
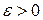выберем 
. Тогда из условий 
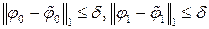будет следовать 
, что и означает непрерывную зависимость решений от начальных данных.
Теорема единственности
Докажем единственность решения задачи Коши для волнового уравнения. Для простоты будем считать 
, что не является ограничением, так как этого можно добиться заменой 
. Для определенности рассмотрим случай трех независимых переменных
(1)
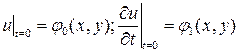(2)
Покажем, что задача Коши (1)-(2) имеет единственное решение в классе дважды непрерывно дифференцируемых функций. Предположим, что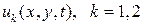 
удовлетворяет (1), (2). Тогда 
будет удовлетворять (1) и условиям
(3)
Покажем, что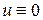 
при 
. Возьмем в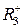 
точку 
, из этой точки, как из вершины, проведем конус
до пересечения с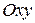 
. Этот конус будем называть характеристическим конусом. Пусть 
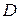- область, ограниченная боковой поверхностью характеристического конуса и частью плоскости 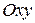, находящейся внутри конуса.
Рассмотрим выражение
и выражение
докажем, что они равны.
Проверяем:
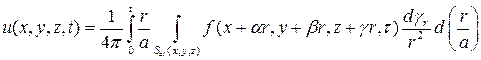
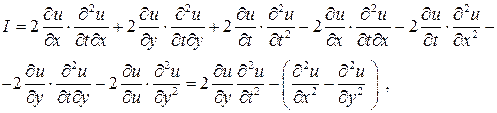
что и требовалось доказать.
Таким образом, справедливо тождество
Проинтегрируем это тождество по области 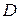. Интеграл от левой части равен 0, так как 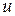- решение уравнения (1).
.
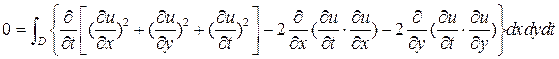Преобразуем этот интеграл в поверхностный по формуле Остроградского. Обозначим 
- боковая поверхность конуса, 
- основание конуса. На в силу (3)
и остается лишь интеграл по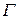 
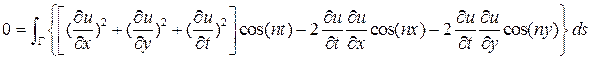. (4)
Отметим, что на боковой поверхности конуса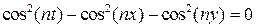 
.
Действительно 
, где 
функция 
.
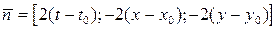
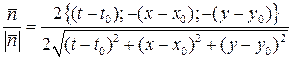
Поэтому
;
;
.
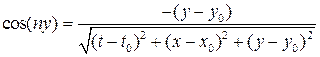на .
Поэтому
(на поверхности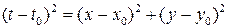 
) 
.
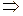
Выбирая внешнюю нормаль, заключаем 
, так как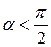 
.
Утверждение. Тождество (4) можно записать в виде
|
.
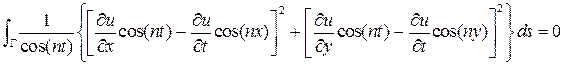Доказательство. Проверим, раскрывая, скобки:
как в (4).
Утверждение доказано.
Подставим в формулу утверждения 
. Так как подынтегральная функция неотрицательна, непрерывна и интеграл равен 0, то на поверхности конуса: (на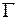 
)
(за исключением 
: 
и 
)
(5)
Обозначим через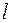 
направление какой-нибудь образующий характеристического конуса. Воспользовавшись (5), получим
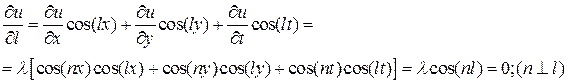
(по непрерывности, и на направлениях, где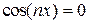 
и 
- результат тот же).
Итак, вдоль любой направляющей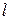 
, 
.
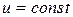В точке, где образующая пересекает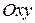 
, значение 
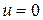, значение 
в вершине конуса 
: 
, что и требовалось доказать.
Замечание. Это утверждение сохраняет силу, если однородные начальные условия (3) имеют место не на всей 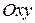, а лишь на основании 
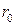области 
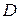. Отсюда можно заключить, что значение решения волнового уравнения (1) в точке 
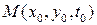зависит от значений начальных данных только на той части плоскости 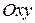, которая вырезается из 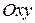характеристическим конусом с вершиной .
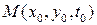Неоднородное волновое уравнение.
Рассмотрим уравнение:
(1)
и будем искать его решение, удовлетворяющее нулевым начальным условиям
(2)
(Добавляя к этому решению решение однородного уравнения, удовлетворяющее неоднородным условиям при 
, получим решение (1) с неоднородными условиями (2)). Для решения (1), (2) рассмотрим вспомогательное однородное уравнение
(3)
удовлетворяющее начальным условиям
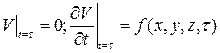(4)
где за начальные моменты взято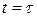 
, 
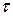- параметр. Решение (3)-(4) будет выражаться формулой Пуассона с заменой 
на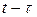 
поскольку начальный момент не , а :
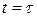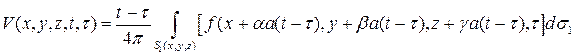. (5)
Покажем, что функция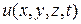 
, определенная формулой
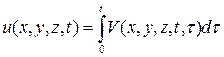(6)
является решением неоднородного волнового уравнения (1) при начальных данных (2).
Действительно, из (6) имеем
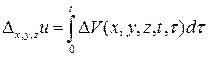(7)
Дифференцируем (6) по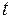 
:
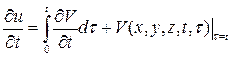(8)
Здесь 
в силу (4). Еще раз дифференцируем по :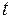
.
Опять, в силу (4):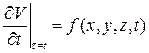 
, то есть
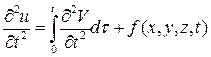(9)
Из (7) и (9) вытекает, что функция (6) удовлетворяет (1). Начальные данные также (2) выполнены, что следует из (6) и (8).
Подставим теперь в формулу (6) вместо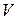 
ее представление (5):
Введем вместо 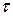новую переменную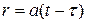 
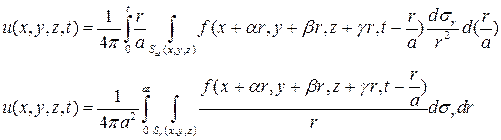
Пусть
(*)
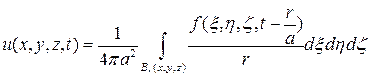(10)
(из (*): 
)
Выражение (10) называется запаздывающим потенциалом.
Замечание. Название обусловлено тем, что при интегрировании, функция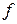 
берется не в момент , а в момент 
, предшествующий моменту , но такой промежуток времени, который потребуется процессу, распространяющемуся со скоростью 
для прохождения от точки 
до 
.
Совершенно так же, как и выше, мы можем получить решение неоднородного волнового уравнения
(11)
удовлетворяющее начальным данным
(12)
Это решение имеет следующий вид
,
где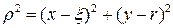 
(доказать самим).
В случае уравнения
решением, удовлетворяющим начальным условиям будет функция
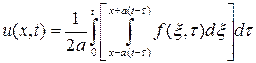
(доказать самим).
Дата добавления: 2015-09-10; просмотров: 70 | Поможем написать вашу работу | Нарушение авторских прав |
