Читайте также:
|
Пусть состояние объекта определяется вектором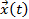 
Переменные 
называются фазовыми переменными. Множество возможных значений фазовых векторов называется фазовыми пространствами. Объект снабжен управляющими устройствами (рулями), направляющая которых определяется
u(t)= 
, u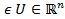 
Множество U называется компактным.
В качестве допустимых управлений принимаются измеримые функции, в частности, кусочно-непрерывные и даже кусочно-постоянные функции.
Движение объекта описывается системой дифференциальных уравнений:
Если 
известно, то с помощью дифференциального уравнения (1), где 
, можно однозначно определить движение объекта.
Говорят, что допустимое управление переводит объект из начального положения 
в конечное положение 
, если существуют решения x=x(t) системы (1), соответствующие выбранному управлению 
, удовлетворяющие условию: 
, 
Если такое управление существует, то он называется оптимальным, а траектория
- оптимальной траекторией.
Принцип максимума дает необходимые условия оптимальности.
Дата добавления: 2015-09-10; просмотров: 219 | Поможем написать вашу работу | Нарушение авторских прав |