Читайте также:
|
Опр: Полугруппа с нейтр эл-ом, каждый элемент которой имеет симметрический, наз группой. Аксиомы группы: (G,*) 1)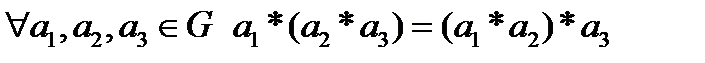 
2) 
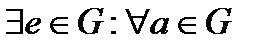e*a=a*e=e 3) 
Если * - комутат опер, то группа назыв комутат или абелевой, Если в группе содерж конечное число элементов, то она наз конечной, а число элементов - порядком полугруппы, в противном случае наз бесконечной.
Свойства групп:
1) В группе сущ и единств е.
2) У произвольно элемента группы сущ единств симметр-кий элем.
3) В аддитивной группе можно опр операцию вычитание, в мультипликативной- деление.
4) В группе решаются ур-ния вида: х*а=b => x=b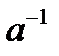 
, a*x=b => x= 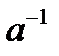b
5) В аддитивной определено целочисленное кратное (-m)a=m(-a) (m>0). В мультипликативной определена целочисленная степень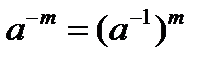 
(m>0) Примеры: 1) G={e},* (e*e=e)
2) G={e,a},* Таблица Кэли: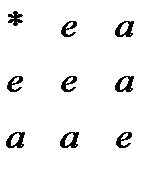 
3) (С(n),•) 4) (Q,•)- не группа т.к. 
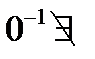(Q\{0},•)- группа.
5) GL(n,R)- общая линейная группа, общая группа всех невырожденных матриц порядка n.
Дата добавления: 2015-09-11; просмотров: 98 | Поможем написать вашу работу | Нарушение авторских прав |