
Читайте также:
|
1. Геометрический.
Найти кривую, при вращении которой вокруг оси x получается наименьшая поверхность вращения.

Этот интеграл не содержит  x, поэтому первый интеграл Лагранжа-Эйлера можно выписать сразу.
x, поэтому первый интеграл Лагранжа-Эйлера можно выписать сразу.

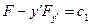

Рис. 6.

 (1)
(1)
Сделаем замену  (
( ) подставим в (1)
) подставим в (1)
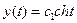

Получим систему:  - цепная линия.
- цепная линия.
 2. Принцип наименьшего действия.
2. Принцип наименьшего действия.
Тело массы m перемещается из точки a в точку b под действием сколь угодно важных внешних сил.
Найти траекторию, по которой произошло движение.
Вместо уравнения Ньютона можно пользоваться более общим принципом наименьшего действия. Рис. 7.
Введем функционал  , где S – действие, а
, где S – действие, а  – это все потенциально возможные траектории, включая истинную. Истинная траектория – это траектория, на которой действие минимально.
– это все потенциально возможные траектории, включая истинную. Истинная траектория – это траектория, на которой действие минимально.
 , где L – это функция Лагранжа.
, где L – это функция Лагранжа.
 ,где T- кинетическая энергия, U- потенциальная.
,где T- кинетическая энергия, U- потенциальная.
Покажем эквивалентность этого принципа и закона Ньютона для движения материальной точки.

Запишем уравнение Лагранжа-Эйлера:
 , где
, где  это
это  .
.
Тогда 

 , т.е. принцип наименьшего действия эквивалентен закону Ньютона для движения материальной точки.
, т.е. принцип наименьшего действия эквивалентен закону Ньютона для движения материальной точки.
Дата добавления: 2015-09-10; просмотров: 77 | Поможем написать вашу работу | Нарушение авторских прав |