Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Гипотеза о существовании вихревого электрического поля

Закон электромагнитной индукции, решающий обратную задачу электромагнетизма — переход от магнитного поля к электрическому току содержит тот же принципиальный недостаток, связанный с экспериментальным происхождением закона: магнитное поле, меняющееся во времени, можно создать в любой среде, а индукционный ток возникает лишь при наличии проводника, в котором могут перемещаться заряды. Возникнут ли те условия, которые приводят в движение свободные заряды и в том случае, если этих зарядов нет? Заряды движутся направленно в том случае, если есть поле , а оно, как и магнитное, может существовать всюду, а не только в проводнике. Следуя этой логике, Максвелл выдвигает предположение, что переменное магнитное поле приводит к появлению поля электрического. Если в это поле внести проводник, заряды начинают двигаться, что мы и обнаруживаем на опыте. Силовые линии этого электрического поля, в отличие от электростатического поля, созданного зарядами, являются замкнутыми кривыми, расположенными в плоскости, перпендикулярной магнитному полю и образуют с ним левовинтовую систему (рис. 4.3).

Сформулированное выше положение вновь гипотетично, требует экспериментального подтверждения и носит название второй Максвелловской гипотезы (1864). Непотенциальность индукционного электрического поля приводит к созданию электродвижущей силы

e .

(4.6)

Это уравнение есть математическая формулировка второй Максвелловской гипотезы.

Гипотеза Максвелла о существовании вихревого электрического поля получила экспериментальное подтверждение позже. В наше время вихревое электрическое поле используется в ускорителях легких частиц — бетатронах.

Совместив уравнение, выражающее гипотезу о существовании электрического поля, с законом электромагнитной индукции, получим

.

(4.7)

Этот обобщённый закон электромагнитной индукции отличается от прежнего тем, что в нём говорится о связи не магнитного поля и тока, а о связи двух полей, которые могут существовать в любой среде.

Вновь используя понятие циркуляции вектора и опираясь на рис. 4.2, можно показать, что переменное во времени магнитное поле приводит к возникновению не постоянного, а переменного по координате электрического поля. Заменим круговой интеграл в левой части (4.7) частными производными:

,

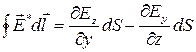(4.8)

где dS есть площадь контура, равная dzdy. Получая (4.8), помните (см. рис. 4.2), что поле , направленное по оси X — переменное, а силовая линия, проведённая через точку А, определяется правилом левого буравчика, как того требует гипотеза. Обход по контуру начат из точки, ближайшей к началу координат.

Заменяя в обобщённом законе электромагнитной индукции интеграл через производные, получим второе Максвелловское уравнение:

.

(4.9)

Вы поняли, конечно, что при переходе от (4.7) к (4.9) в правой его части поток был выражен через магнитную индукцию, а она, в свою очередь, заменена напряжённостью Н. Уравнение вновь получено для двумерного случая, представляет обобщение закона электромагнитной индукции и содержит утверждение, что меняющееся во времени магнитное поле приводит к появлению меняющегося по координате электрического поля.

Обратите внимание на то, что поля перпендикулярны друг другу, а ток i на рис. 4.2 не может быть постоянным, иначе напряжённость магнитного поля тоже будет постоянной и вихревое электрическое поле не возникнет.