Читайте также:
|
В отсутствие внешнего магнитного поля парамагнитные молекуы, составляющие какое-либо вещество, вследствие теплового движения ориентированы совершенно беспорядочно, а диамагнитные молекулы вообще не обладают магнитным моментом. Поэтому сумма магнитных моментов молекул, заключенных в некотором физически бесконечно малом объеме dV, будет равна нулю:
ådV р тi. =0
Под действием внешнего магнитного поля парамагнитные молекулы ориентируются преимущественно по полю, несмотря на то, что тепловое движение стремится разупорядочить их ориентацию. Диамагнитные молекулы во внешнем поле намагничиваются. Таким образом, какие бы молекулы ни входили в состав вещества, если его поместить в магнитное поле, сумма магнитных моментов всех молекул в любом физически бесконечно малом объеме dV уже не будет равна нулю. Вещество в таком состоянии называется намагниченным. Состояние намагниченного вещества характеризуется вектором
J =ådV р тi /dV
который называется намагниченностью. По определению вектор J есть магнитный момент единицы объема намагниченного вещества. В этом заключается физический смысл этого вектора.
Намагниченность различных областей вещества может быть неодина
ковой. В таком случае вектор намагниченности будет зависеть от коор
динат точки пространства:
J = J (r),_
Намагниченность вещества называется однородной, если вектор J во всех его точках один и тот же. Намагниченность физически бесконечно малого объема вещества всегда можно считать однородной.
Токи, обусловленные движением электронов в атомах и молекулах, называют молекулярными, или связанными токами. Токи проводимости и конвекционные токи называют свободными. Силы молекулярных токов будем обозначать I', а свободных - I*.
7.3. Циркуляция вектора намагниченности *
Будем упрощенно рассматривать каждую молекулу как круговой контур с током I', площадь которого обозначим Sm. Все молекулы будем считать одинаковыми и в среднем одинаково ориентированными в пространстве. В этом случае из определения (7.2) следует, что
J =n p m, (7.3)
где п - концентрация молекул; р т - магнитный момент одной молекулы,
pm = I'Sm. (7.4)
Построим в пространстве, где имеются молекулы некоторого вещества, произвольный контур С (рис. 7.2). Вычислим сумму молекулярных токов
Рис. 7.2. К вычислению суммы молекулярных токов,
охватываемых контуром С
Контур С охватывает только те молекулярные круговые токи, которые "нанизаны" на него (рис. 7.2).
(7.5)
|
Рис. 7.3. Молекулярный ток, "нанизанный" на вектор dl
Найдем сначала сумму молекулярных токов, "нанизанных" на векторный элемент dl контура С. На вектор dl "нанизаны" молекулярные токи, центры которых находятся внутри косого цилиндра (рис. 7.3). Их число равно произведению концентрации п молекул на объем Smcos a dl цилиндра. Если все молекулярные токи одинаковы, то сумма токов, "нанизанных" на вектоp dl будет
пI'Sm cos adl.
Произведение пI'Sm есть модуль вектора J.
J = пI'Sm
Поэтому сумму молекулярных токов, "нанизанных" на вектор dl, можно записать как скалярное произведение Jdl, а сумму всех молекулярных токов, "нанизанных" на контур С, представить как циркуляцию вектора
J по этому контуру:
å I' = 
7.4. Напряженность магнитного поля
В сумму, стоящую в правой части уравнения (6.8), входят все токи, охватываемые контуром С: и свободные, и молекулярные. С учетом разделения токов на эти две категории запишем уравнение (6.8) так:
= μo (å I* +å I')
Исключив при помощи равенства (7.5) сумму å I'
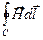= å I*
|
Вектор
H = B / μo - J
называют напряженностью магнитного поля. Согласно равенству (7.7) циркуляция вектора напряженности по произвольному контуру равна алгебраической сумме свободных токов, охватываемых этим контуром.
Когда свободные токи текут в сплошной среде, сумму в правой части уравнения (7.7) следует заменить интегралом
å I* = 
где j* - плотность свободных токов; S - поверхность, натянутая на контур С. При этом уравнение (7.7) примет вид (7.9)
|
где направления векторов dl и dS связаны правилом правого винта.
Преобразовав криволинейный интеграл в левой части уравнения (7.9) по теореме Стокса (6.42) в поверхностный интеграл от ротора напряженности магнитного поля, придем к дифференциальному уравнению
rot H = j*
В большинстве задач теории постоянного магнитного поля свободные токи считаются известными. Преимущество уравнений (7.7), (7.9) и (7.10)
для вектора Н перед уравнениями (6.8), (6.11) и (6.13) для вектора В заключается в том, что они не содержат величин, характеризующих молекулярные токи, которые чаще всего бывают неизвестны.
Дата добавления: 2015-09-11; просмотров: 84 | Поможем написать вашу работу | Нарушение авторских прав |