Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Расчет индукции магнитного поля на оси соленоида

Получим формулу для индукции магнитного поля на оси соленоида длины l и радиуса а, на единицу длины которого приходится п витков (рис. 6.6). Пусть в соленоиде идет ток, сила которого равна I.

l

Рис.6.10.К расчету индукции магнитного поля на оси соленоида

Будем рассматривать соленоид как совокупность узких колец с током. Одно из таких колец показано на рис. 6.10. Положение этого кольца определяется координатой x, которая изменяется в пределах от 0 до l, а его ширина равна dx. Так как рассматриваемое кольцо содержит ndx витков, круговой ток, текущий по кольцу, имеет силу

di =Indx. (6.26)

Этот ток создает магнитное поле, индукцию dB которого в на оси соленоида можно найти по формуле(6.24)

dВ = μ_oa²di/ (2 R ³) (6.27)

где расстояние от точки Р до кольца с током

R =Ö(a² +(x-x)²)

х - координата точки Р.

Индукция В магнитного поля, создаваемого в точке Р всеми витками соленоида, в силу принципа суперпозиции равна интегралу от выраже­ния (6.27):

В = μ_oIn a²/ 2

Для вычисления этого интеграла удобно ввести новую переменную нтегрирования - угол q. Как видно из рис. 6.10, уголqтаков, что

R = adq/sin q (6.29)

и

x- х = a ctgq (6.30)

Продифференцировав равенство (6.30) при х = const, получим

dx = adq/sin²q (6.31)

Подстановка выражений (6.29) и (6.31) под знак интеграла в формуле (6.28) дает

В(x) = μ_oIn / 2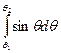

где q₁ и q₂ - наибольшее и наименьшее значения угла q, зависящие от положения точки Р на оси соленоида. Интегрирование по формуле Ньютона - Лейбница приводит к выражению

(6.32)

Выразим cos q₁ и cos q ₂ через х для значений х, удовлетворяющих не­равенству

0 < х < l,

т.е. для точек, лежащих на оси х внутри соленоида. Из построений на

рис. 6.11 найдем, что

cos q₁ =

cos q₂ =

Подставив эти выражения в формулу (6.32), будем иметь зависимость

В(x) = μ_oIn / 2( + ) 6.33)

Эта формула дает следующие значения магнитной индукции на торцах соленоида и в его середине:

B(0) = В(l) =

В(l/2 =)

где D = 2 a - диаметр соленоида.

Нетрудно убедиться в том, что формула (6.33) справедлива для всех точек на оси соленоида. Согласно этой формуле магнитная индук­ция монотонно убывает до нуля при | х |® + ¥. График зависимости В = В(х), определяемый формулой (6.33), изображен на рис. 6.12. Интересно отметить, что при l|® + ¥ формула для магнитной В(l/2) ин­дукции в середине соленоида переходит в полученное ранее выражение В=μ_oIn для магнитной индукции внутри бесконечного соленоида.

Рис. 6.11. К вычислению магнитной индукции поля в соленоиде

В(х)

B(0)

l x

Рис. 6.12. Магнитная индукция на оси соленоида