Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Магнетизм

§ 1. Магнитное поле. Закон Ампера

Между проводниками с током существует взаимодействие, называемое магнитным. Осуществляется взаимодействие посредством магнитного поля: один проводник с током создает в пространстве магнитное поле , другой проводник находится в этом поле. На элемент тока I в магнитном поле действует сила Ампера

. (1)

На проводник с током конечной длины действует сила

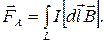(2)

Вектор называется вектором индукции магнитного поля.

§ 2. Закон Био-Савара-Лапласа

Принцип суперпозиции для вектора

Элемент тока I проводника с током создает в т.А с радиусом вектором 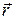магнитное поле , вычисляемое в соответствии с законом Био-Савара-Лапласа по формуле

. (1)

Все элементы тока, из которых состоит проводник с током, создают поле

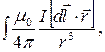(2)

что соответствует принципу суперпозиции для магнитного поля

(3)

§ 3. Применение принципа суперпозиции

для вычисления индукции магнитного поля

3. Магнитное поле прямого тока I.

Все d всех элементов тока I направлены одинаково, поэтому ; B = .

dB =

B =

B = . (1)

Поле направлено по касательной к окружности в т.А.

4. Магнитное поле на оси кругового тока.

dB _z = dB ·cosa B _z = = .

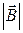dB _z = :

B =

r ² = R ² + Z²; cosa =

B = . (2)

Поле направлено по оси Z.

3. Вычислив с помощью принципа суперпозиции поле во всем пространстве, можно найти силу взаимодействия токов по формуле (1.2).

§ 4. Взаимодействие параллельных токов.