Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Индуктивность коаксиального кабеля

Коаксиальный кабель представляет собой два длинных соосных прово­дящих цилиндра, пространство между которыми заполнено каким-либо изолирующим материалом с магнитной проницаемостью m. Пусть а - радиус внутреннего цилиндра, а b - внешнего. Длина кабеля обычно во много раз превышает его радиус. Поэтому магнитное поле, создава­емое электрическим током в кабеле, будет таким же как у бесконечно длинного кабеля, если не учитывать искажения поля у его концов.

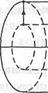
Найдем индуктивность участка кабеля длиной l. Для этого создадим замкнутую электрическую цепь из внутреннего и внешнего цилиндров кабеля и подключим к этой цепи источник постоянной ЭДС (рис. 8.6, а).Токи, создаваемые этой ЭДС, потекут по поверхностям цилиндров вдоль их оси в противоположных направлениях.

В силу цилиндрической симметрии системы силовые линии магнит­ного поля суть семейство окружностей, центры которых лежат на оси симметрии. На рис. 8.6, а изображена одна из силовых линий. Для определения напряженности магнитного поля применим теорему (7.7) о циркуляции вектора Н. В качестве контура интегрирования С выберем силовую линию произвольного радиуса г. Циркуляция вектора напря­женности по такому контуру буд

Hdl = H dl = H dl = Н 2pr. (8.33)

H

Рис. 8.6. Коаксиальный кабель

Если радиус контура С меньше радиуса внутреннего цилиндра (г < а), то внутри контура С ток не протекает. В случае, когда кон­тур С охватывает оба цилиндра (г > 6), сумма токов равна нулю, так как токи в цилиндрах имеют противоположные направления. Поэтому напряженность магнитного поля Я = 0 при г < а и г > Ь, т.е. магнитное поле внутри малого цилиндра и вне большого отсутствует. Если радиус контура С таков, что а < г < Ь, то такой контур охватывает только ток во внутреннем цилиндре. При этом по теореме (7.7) циркуляция (8.32) будет равна силе тока / в рассматриваемой цепи:

2prН = I.

Таким образом, напряженность магнитного поля внутри коаксиального кабеля

Н = I /2pr.

Плотность энергии магнитного поля в пространстве, где а < r < b, найдем по формуле (8.28):

w = (1/2) mH² = (1/2) m I² /8p² r². (8.35)

Найдем энергию магнитного поля внутри кабеля. Для этого рассмо­трим цилиндрический слой, образованный двумя воображаемыми цилин­драми радиусов r и r + dr (рис. 8.6, б).Если длина слоя равна l, то его объем dV = 2prldr. Так как плотность энергии (8.35) зависит только от г, внутри тонкого цилиндрического слоя она будет всюду одна и та же. Поэтому энергия магнитного поля в слое

dW = w(r) dV = (1/2)(m I² / (8p 2r²))2 prldr

.

Проинтегрировав это выражение по r в пределах от а до b, найдем энер­гию магнитного поля на участке кабеля длиной l:

W = (1/4 p) m I²l = (1/4 p) m I²l ln(b/a) (8.36)

С другой стороны, энергию магнитного поля можно определить по формуле (8.26). Приравняем эти выражения и найдем индуктивность участка коаксиального кабеля длиной l:

L= 2W/I² =(1/2 p) m l ln (b/a) (8.37)