Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Энергия магнитного поля

Рассмотрим цепь, состоящую из проводика сопротивлением R и катуш­ки с постоянной индуктивностью L (рис. 8.4). Пусть в момент времени t = 0 в этой цепи протекает электрический ток силой I₀. Найдем, как ток будет меняться при t > 0. Для этого запишем второе правило Кирхгофа, согласно которому сумма падений напряжений в контуре равна сумме ЭДС. В рассматриваемом контуре напряжение падает на проводнике, а в катушке возникает электродвижущая сила самоиндукции. Таким образом,

RI = -LdI/dt,

Это есть уравнение с разделяющимися переменными, т.е. его можно за­писать так:

dI/I = - (R/ L) dt (8.22)

После интегрирования получим

I(t) = I₀ exp(-Rt/L) (8.23)

Из этой формулы следует, что ток в цепи, содержащей катушку индук­тивности, не может прекратиться мгновенно. Уменьшение силы тока приводит к возникновению электродвижущей силы самоиндукции в ка­тушке, которая согласно правилу Ленца препятствует исчезновению то­ка.

Рис. 8-4- Электрический ток в этом контуре поддерживается благодаря ЭДС самоиндукции

Умножим уравнение (8.22) на I. После простого преобразования правой части будем иметь

RI² = - (8.24)

Левая часть этого равенства есть мощность джоулева энерговыделе­ния, т.е. количество тепла, которое выделяется на сопротивление за единицу времени при прохождении по нему электрического тока. Что является источником энергии, которая расходуется на нагревание про­водника? В рассматриваемом контуре нет других элементов, кроме со­противления и катушки. Поэтому приходим к выводу, что в катушке, а также в любом проводящем контуре с током запасается энергия, кото­рая, как следует из равенства (8.24), определяется соотношением

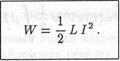
- энергия магнитного поля. (8.25)

Равенство (8.24) выражает собой закон сохранения энергии. Производная - W¢ есть количество энергии, которое теряется катушкой за единицу времени. Согласно равенству (8.24) эта энергия равна количеству тепла, выделяющемуся в сопротивлении за это время.

Пусть катушка является соленоидом, индуктивность которого опреде­ляется формулой (8.21):

L=mn²V. (8.26)

Согласно (8.25) и (8.26) в соленоиде с током I запасена энергия

W= (1/2) mn²I²V.

В силу (7.17) произведение nI равно напряженности H магнитного поля внутри соленоида, поэтому

W = (1/2) mH²V

Энергия (8.27) зависит от напряженности Я магнитного поля внутри со­леноида, от магнитной проницаемости среды, заполняющей пространство внутри соленоида, и пропорциональна его объему. Отсюда можно заклю­чить, что носителями этой энергии являются магнитное поле и намаг­ниченное вещество. Так как поле внутри длинного соленоида, заполнен­ного однородным веществом, также однородно, энергия W равномерно распределена в пространстве соленоида и пропорциональна его объему V. В этом случае объемная плотность энергии w равна отношению энер­гии W к объему V:

w = (1/2) mH² (8.28)

Эта формула справедлива также в общем случае, т.е. и тогда, когда маг­нитное поле неоднородно. При этом энергия поля в малом объеме равна произведению плотности энергии (8.28) на величину dV этого объема:

dW = w(r)dV = (1/2) mH²dV

Энергия поля в объеме Vвыражается интегралом

W = ò_V w(r)dV = (1/2)ò_V mH²dV

ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ (продолжение)