Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Методы отсечения. Метод Гомори

Сущность методов отсечения состоит в том, что сначала задача решается без условия целочисленности. Если полученный план целочисленный, то задача решена. В противном случае к ограничениям задачи добавляется новое ограничение, обладающее следующими свойствами:

- оно должно быть линейным;

- должно отсекать найденный оптимальный нецелочисленный план;

- не должно отсекать ни одного целочисленного плана.

Дополнительное ограничение, обладающее указанными свойствами, называется правильным отсечением.

Далее задача решается с учетом нового ограничения. После этого в случае необходимости добавляется еще одно ограничение и так далее.

В результате новый многогранник решений содержит все целые точки, заключавшиеся в первоначальном многограннике решений и, соответственно, полученное при этом многограннике оптимальное решение будет целочисленное (рис. 4.5).

Один из алгоритмов решения задачи линейного целочисленного программирования (4.41) – (4.44), предложенный Гомори, основан на симплексном методе и использует достаточно простой способ построения правильного отсечения.

Пусть задача линейного программирования (4.41) – (4.43) имеет конечный оптимум и на последнем шаге ее решения симплексным методом получены следующие уравнения, выражающие базисные переменные x₁, x₂,..., x_j,..., x_m через свободные переменные x_m+1, x_m+2,..., x_m+i,..., x_n оптимального решения

x₁ = b₁ – a_1,m+1ּ x_m+1 -... – a_1,m+iּ x_m+i -... – a_1,nּ x_n

x₂ = b₂ – a_2,m+1ּ x_m+1 -... – a_2,m+iּ x_m+i -... – a_2,nּ x_n

.......

x_i = b_i – a_i,m+1ּ x_m+1 -... – a_i,m+iּ x_m+i -... – a_i,nּ x_n (4.45)

.......

x_m = b_m – a_m,m+1ּ x_m+1 -... – a_m,m+iּ x_m+i -... – a_m,nּ x_n

так, что оптимальным решением задачи (4.41) – (4.43) является

X* = (b₁, b₂,..., b_i,..., b_m, 0, 0,..., 0), в котором, например, b_i – нецелая компонента. В этом случае можно доказать, что неравенство¹⁾

{b_i} – {a_i,m+1}ּx_m+1 -... – {a_i,m+i}ּx_m+i -... – {a_i,n}ּ x_n ≤ 0 (4.46)

сформированное по i-му уравнению системы (4.45), обладает всеми свойствами правильного отсечения.

--------------------------------------------------------------------------------------------------------

1) – в неравенстве (4.46) символ { } означает дробную часть числа. Целой частью числа а называется наибольшее число [a], не превосходящее а, а дробной частью числа – число {а}, равное разности между этим числом и его целой частью, то есть, {а} = а - [a].

Например, для а = 2 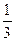имеем [a] = 2, {а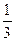} = 2 - 2 = ;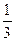

для а = - 2 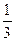имеем [a] = -3 {а} = - 2 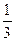- (-3) = ;

--------------------------------------------------------------------------------------------------------

Для решения задачи целочисленного линейного программирования

(4.41) – (4.44) методом Гомори используется следующий алгоритм:

1. Симплексным методом решить задачу (4.41) – (4.43) без учета условия целочисленности. Если все компоненты оптимального плана целые, то он является оптимальным и для решения задачи целочисленного программирования (4.41) – (4.44). Если первая задача (4.41) – (4.43) неразрешима (то есть, не имеет конечного экстремума или условия ее противоречивы), то и вторая задача

(4.41) – (4.44) также неразрешима.

2. Если среди компонент оптимального решения есть нецелые, то выбрать компоненту с наибольшей целой частью и по соответствующему уравнению системы (4.45) сформировать правильное отсечение (4.46).

3. Неравенство (4.46) введением дополнительной неотрицательной переменной преобразовать в равносильное уравнение

{b_i} – {a_i,m+1}ּx_m+1–... –{a_i,m+i}ּx_m+i –... – {a_i,n}ּx_n + x_n+1 = 0 (4.47)

и включить его в систему ограничений (4.42).

4. Полученную расширенную задачу решить симплексным методом. Если найденный оптимальный план будет целочисленным, то задача целочисленного программирования (4.41) – (4.43) решена. В противном случае вернуться к п. 2 алгоритма.

Если задача разрешима в целых числах, то после конечного числа шагов (итераций) оптимальный целочисленный план будет найден.

Если в процессе решения появится уравнение (выражающее базисную переменную через свободные) с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.

Недостатком метода Гомори является требование целочисленности всех переменных: как основных, выражающих единицы продукции, так и для дополнительных, выражающих величину неиспользованных ресурсов, которые могут быть и дробными.

Пример 4.1. Для приобретения оборудования по сортировке зерна фермер выделяет 34 ден.ед. Оборудование должно быть размещено на площади, не превышающей 60 кв. м. Фермер может заказать оборудование двух видов: менее мощные машины типа А стоимостью 3 ден.ед., требующие производственную площадь 3 кв. м. (с учетом проходов) и обеспечивающие производительность за смену 2 т. зерна, и более мощные машины типа В стоимостью 4 ден.ед., занимающие площадь 5 кв.м. и обеспечивающие производительность за смену 3 т. сортового зерна.

Требуется составить оптимальный план приобретения оборудования, обеспечивающего максимальную общую производительность при условии, что фермер может приобрести не более 8 машин типа В.

Решение. Обозначим через х₁, х₂ количество машин, соответственно, типа А и В, через Ф – общую производительность. Тогда математическая модель задачи примет вид: Ф = 2 x₁ + 3 x₂ → max (4.1.1)

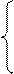при ограничениях: 3 x₁ + 5 x₂ ≤ 60,

3 x₁ + 4 x₂ ≤ 34, (4.1.2)

x₂ ≤ 8,

х₁≥ 0, х₂ ≥ 0, (4.1.3)

х₁, х₂ - целые числа., (4.1.4)

Приведем задачу к каноническому виду, введя дополнительные неотрицательные переменные х₃, х₄, х₅ . Получим систему уравнений:

3 x₁ + 5 x₂ + х₃ = 60,

3 x₁ + 4 x₂ + х₄ = 34, (4.1.5)

x₂ + х₅ = 8,

х_j≥ 0, j=1, 2, …, 5.

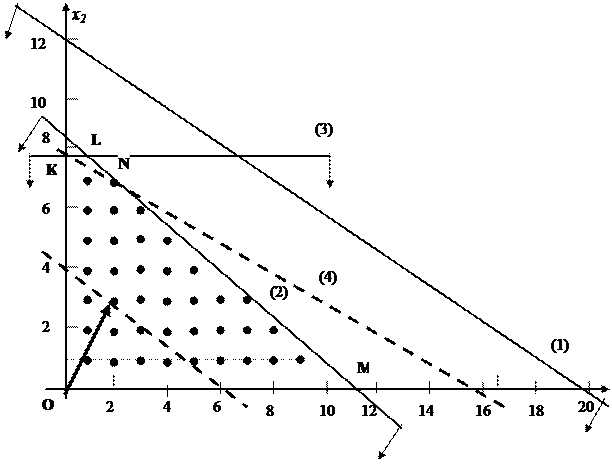
Решаем задачу симплексным методом. Для наглядности решение проиллюстрируем графически (рис. 4.2).

		х1

Рис. 4.2.

На рис. 4.2 OKLM–область допустимых решений задачи (4.1.1) –(4.1.3), ограниченная прямыми (1), (2), (3) и осями координат; L(2/3; 8) – точка оптимального, но нецелочисленного решения задачи (4.1.1)–(4.1.3); (4) - прямая, отсекающая это нецелочисленное решение; OKNM – область допустимых решений расширенной задачи (4.1.1) – (4.1.3), (4.1.4); N(2; 7) – точка оптимального целочисленного решения.

I шаг. Базисные переменные х₃, х₄, х₅; свободные переменные х₁, х₂.

х₃ = 60 - 3 x₁ - 5 x₂ ,

х₄ = 34 - 3 x₁ - 4 x₂,

х₅ = 8 - x₂,

Ф = 2 x₁ + 3 x₂ ,

Первое базисное решение Х₁ = (0; 0; 60; 34; 8) – допустимое. Соответствующее значение линейной функции Ф₁ = 0.

Условие оптимальности не выполнено, максимум Ф не достигнут. Переводим в базисные переменную x₂, которая входит в выражение линейной функции с наибольшим положительным коэффициентом. Находим максимально возможное значение x₂, которое «позволяет» принять система ограничений, из условия минимума соответствующих отношений x₂ = min (60/5; 34/4; 8/1) = 8,

то есть, разрешающим является третье уравнение. При x₂ = 8 в этом уравнении х₅= 0, и в свободные переходит переменная х₅, переменная x₂ - в базисные.

II шаг. Базисныепеременные х₂ , х₃ , х₄; свободные переменные х₁ , х₅.

х₂ = 8 – x₅

х₃ = 20 - 3 x₁ + 5 x₅ ,

х₄ = 2 - 3 x₁ + 4 x₅ ,

Ф = 24 +2 x₁ - 3 x₅ .

Х₂ = (0; 8; 20; 2; 0); Ф₂ = 24. Условие оптимальности не выполнено, максимум Ф не достигнут. Переводим в базисные переменные х₁ , а в свободные х₄ , так как x₁ = min (∞; 20/3; 2/3) = 2/3,

III шаг. Базисныепеременные х₁ , х₂ , х₃; свободные переменные х₄ , х₅.

х₁= 2/3 – 1/3∙x₄ +4/3∙x₅ ,

х₂ = 8 - x₅ ,

х₃ = 18 + x₄ + x₅ ,

Ф = 76/3 – 2/3 ∙x₄ -1/ 3 ∙x₅ .

Х₃ = (1; 8; 18; 0; 0); Ф₂ = 76/3.. Условие оптимальности выполнено, максимум Ф достигнут, задача решена.