Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Алгебраическая структура циклических кодов

В кодовых словах, выраженных в полиномиальной форме, циклическая природа кода проявляется следующим образом. Если является кодовым словом, представленным полиномом порядка , то — остаток от деления на — также является кодовым словом. Иными словами,

или, умножая обе части уравнения на ,

что в модульной арифметике можно описать следующим образом.

Здесь "х по модулю у" означает остаток от деления х на у. Ниже справедливость выражения демонстрируется для случая i = 1

К последнему выражению прибавим и вычтем или, поскольку мы пользуемся арифметическими операциями по модулю 2, можем прибавить дважды.

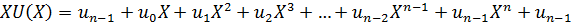
Поскольку порядок равен , этот полином не делится на 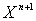, можно записать следующее.

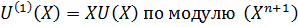
Обобщая, приходим к уравнению.

Пример 6.7. Циклический сдвиг вектора кода

Пусть U = 1 1 0 1 для n = 4. Выразите кодовое слово в полиномиальной форме и выполните третий циклический сдвиг кодового слова.

Решение

полином записан в порядке возрастания степени

, где

Разделим на 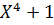и найдем остаток, используя полиномиальное деление.

Записываем остаток в порядке возрастания степеней: 1 + X² + X³, кодовое слово U=1011 представляет собой три циклических сдвига U= 1 1 0 1. Напомним, что для двоичных кодов операция сложения выполняется по модулю 2, так что + 1 = -1, и, следовательно, в расчетах знаки "минус" не отражены.