Студопедия
Главная страница | Контакты | Случайная страница

АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Балансовый метод

Читайте также:
  1. A. гностическим методам
  2. Amp;Сравнительная характеристика различных методов оценки стоимости
  3. C) Методы стимулирования поведения деятельности
  4. E) мировоззренческая, гносеологическая, методологическая.
  5. I ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
  6. I. Из истории развития методики развития речи
  7. I. ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
  8. I. Определение эпидемического процесса и методологическое обоснование разделов учения об эпидемическом процессе.
  9. I. Определение эпидемического процесса и методологическое обоснование разделов учения об эпидемическом процессе.
  10. I. ОРГАНИЗАЦИОННО-МЕТОДИЧЕСКИЙ РАЗДЕЛ
Вариант Заданы двоичные числа X и Y. Вычислить X+Y и X–Y, если: Заданы двоичные числа X и Y. Вычислить X*Y и X/Y, если:
1. Х=100101,1012 Y=11101,112 X=100101,0112 Y=110,12
2. Х=101101,1012 Y=1101,1112 X=110000,112 Y= 2
3. Х=110101,1012 Y=11101,112 X=111001,00012 Y=1010,0112
4. Х=1101111,1012 Y=10101,112 X=111011,00012 Y=101,012
5. Х=1000111,112 Y=11101,1112 X=111100,0112 Y=101,112
6. Х=1110001,1012 Y=10011,112 X=110110,1012 Y=100,112
7. Х=1010001,1012 Y=10011,112 X=100110,00012 Y=111,012
8. Х=1000011,1012 Y=10011,0112 X=101011,1112 Y=110,112
9. Х=1101001, 1012 Y=10111,112 X=1010110,1012 Y=1000,012
10. Х=1010001,1012 Y=1111,0112 X=111111,012 Y=101,12
11. Х=101001, 1012 Y=10111,1112 X=1011010,1012, Y=111,012
12. Х=1010111, 1012 Y=11100,1112 X=1000101,00112, Y=110,112
13. Х=110101,1012 Y=1111,112 X=100101,0112, Y=110,12
14. Х=101111,1012 Y=1101,1112 X=100000,11012, Y=101,012
15. Х=110101,0112 Y=10011,112 Х=110111,112 Y=101,112
16. Х=1001011,112 Y=10101,1012 Х=100101,112 Y=111,012
17. Х=100011,0112 Y=10011,1112 Х=100011,012 Y=1011,12
18. Х=1010001,1012 Y=1011,0112 Х=100001,1012 Y=1001,012
19. Х=110001,1012 Y=10111,112 Х=111001,1012 Y=1101,112
20. Х=1000111,0112 Y=11111,112 Х=1010111,0112 Y=111,112
21. Х=111001, 1012 Y=1110,1112 Х=11100001, 1012 Y=110,112
22. Х=100001,1012 Y=1111,1112 Х=1000001,1012 Y=1111,012
23. Х=1011101, 1012 Y=10111,0112 Х=1010101, 1012 Y=100,0112
24. Х=1111000, 1012 Y=101111,112 Х=1111001, 0112 Y=1011,112
25. Х=1100000, 1012 Y=1111,1112 Х=1100011, 012 Y=11,1112

 

Контрольные вопросы.

1. Каковы правила сложения двоичных чисел?

2. Каковы правила вычитания двоичных чисел?

3. Каковы правила умножения двоичных чисел?

4. Каковы правила вычитания двоичных чисел?

 

 

Балансовый метод

ОН + П = Р + ОК, где

 

ОН - запасы или остатки на начало периода;

ОК - запасы или остатки на конец периода;

П - поступление;

Р - расход, в т.ч. реализация.

 
 

 

 


Метод оптимизации плановых решений

 

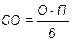
Наиболее вероятное значение прогноза = ОП ± 2СО (границы прогноза).

Экономико-математические методы


Экономико-аналитические (статистические) методы



Дата добавления: 2014-11-24; просмотров: 176 | Поможем написать вашу работу | Нарушение авторских прав
<== предыдущая лекция | следующая лекция ==>
Методические указания.| Факторы, влияющие на цену лекарств
lektsii.net - Лекции.Нет - 2014-2025 год. (0.761 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав