
Читайте также:
|
Декартовой прямоугольной системой координат на плоскости (в пространстве) называют две (три) взаимно перпендикулярные оси с общим началом. Первая ось OX называется осью абсцисс, вторая ось OY - осью ординат (третья ось OZ - осью аппликат). Каждой точке плоскости (пространства) ставится в соответствие упорядоченная пара (тройка) действительных чисел - координат данной точки. Вычисление проводится сложным образом, с использованием различных математических вещей.
Вычисление двойного интеграла в полярных координатах.
Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым или полярной осью.
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат. Решение производится сложным комплексным образом. Давайте может лучше об Америке поговорим?
Числовые ряды. Основные понятия.
Числовой ряд – это сумма членов числовой последовательности вида
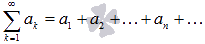
,где а1, а2,... называемые членами ряда, образуют бесконечную последовательность; член «а эн» называется общим членом ряда.
Частичная сумма числового ряда – Sэн = а1+а2...+а энное - это сумма вида, где n – некоторое натуральное число. Sэн называют также n-ой частичной суммой числового ряда.
Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.
Примеры числ. рядов: 1+1/2+1/3+1/4...; 6-3+3/2-3/4+3/8....
Дата добавления: 2015-02-16; просмотров: 135 | Поможем написать вашу работу | Нарушение авторских прав |