Главная страница | Контакты | Случайная страница Автомобили Астрономия Биология География Дом и сад Другие языки Другое Информатика История Культура Литература Логика Математика Медицина Металлургия Механика Образование Охрана труда Педагогика Политика Право Психология Религия Риторика Социология Спорт Строительство Технология Туризм Физика Философия Финансы Химия Черчение Экология Экономика Электроника

Степенные ряды на комплексной плоскости

Степенным рядом называется функциональный ряд вида

(1)

где a₀, a₁,… - вещественные числа, называемые коэффициентами ряда.

Любой степенной ряд сходится в точке х = 0.

Ряды можно рассматривать как в вещественной (действительной), так и в комплексной области.

В комплексной области множество сходимости ряда – внутренность круга радиуса r. Граничные точки этого круга могут как принадлежать, так и не принадлежать области сходимости ряда.

Область сходимости ряда может вырождаться в точку (r = 0), во всю прямую в случае действительного переменного или во всю комплексную плоскость (r = ∞).

Обыкновенные дифференциальные уравнения. Основные понятия.

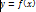Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные , т. е. уравнение вида:

Это дифференциальные уравнения для функции от одной переменной. (Этим оно отличается от уравнения в частных производных, где неизвестная - это функция нескольких переменных.)

Порядком уравнения называется максимальный порядок n входящей в него производной (или дифференциала).

Частным решением уравнения на интервале (a, b) (конечном или бесконечном) называется любая n раз дифференцируемая функция у=ф(х), удовлетворяющая этому уравнению, т.е. обращающая уравнение на этом интервале в тождество.

ДУ первого порядка. Основные понятия.

Уравнение F(x, y, y ') = 0, где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b).

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ') = 0, удовлетворяющего условию y(x0) = y0, называется задачей Коши (или начальной задачей).

Условие y(x0) = y0 — начальное условие.

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называется общим интегралом уравнения.

Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называется частным интегралом уравнения.